Explore every episode of Modellansatz
| Pub. Date | Title | Duration | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 29 Sep 2016 | Erasmus | 00:35:32 | |||||||||||||||||
Vojtěch Cvrček ist im Herbst 2013 als Erasmusstudent von der CTU in Prag nach Karlsruhe ans KIT entsandt worden. Er hatte schon in der Grundschule Deutsch gelernt und wollte seine Sprachkenntnisse direkt in Deutschland verbessern. Deshalb wollte er auch ein ganzes Jahr bleiben (nicht nur ein Semester). Das bedeutete insbesondere, dass er die Einarbeitung in seine Masterarbeit schon in Karlsruhe beginnen müsste und deshalb ein Thema und ein Betreuerteam finden müsste, dass dies ermöglicht. Seine deutsche Wunschstadt war eigentlich Berlin - wegen der räumlichen Nähe zur Prag und weil ihm die Stadt gut gefiel. Leider gab es im Rahmen des Erasmusprogrammes aber keine Möglichkeit für ihn, dort sein Mathematikstudium fortzuführen. Infrage kamen dafür nur die TU Hamburg, TU Darmstadt und das KIT in Karlsruhe. Unter seinen Professoren und Mitstudenten in Prag war das KIT in Karlsruhe nicht gut bekannt, aber ein ordentlicher Fußballverein war in seinen Augen ein Pluspunkt für Karlsruhe. Nach der Entscheidung für Karlsruhe suchte er nach persönlichen Ansprechpartnern. Er fand die Projekte von Matthias Krause im Internet und ihn begeisterte insbesondere die dort vorgestellte Zusammenarbeit der Mathematik mit dem studentischen Projekt KAraceing. Deshalb schrieb er Matthias Krause eine e-mail und stellte sich als künftiger Erasmusstudent vor, der den einen oder anderen Rat einholen wollen würde. Er fand ein offenes Ohr und geeignete Lehrveranstaltungen wurden entsprechend seinen Zielen für das Jahr in Karlsruhe zusammengestellt. Für die Zeit in Karlsruhe und darüber hinaus hatte er damit einen Mentor, der ihn schließlich auch in seine Arbeitsgruppe integriert hat. Vojtěch Cvrček wurde studentische Hilfskraft und unterstützte Matthias Krause zunächst in der Lehre bis er in der Lage war, das Softwareprojekt OpenLB mit weiter zu entwickeln. Die Gruppenmeetings des Teams um OpenLB gehörten selbstverständlich zu seiner Arbeit und der Austausch in der Gruppe war dadurch sehr intensiv. Deshalb sieht Vojtěch Cvrček das Jahr in Karlsruhe als das beste Jahr in seinem Studium an. Er hat hier sehr viel gelernt und tolle Unterstützung durch Mitstudierende gefunden. Als Vorlesungen entschied er sich für Mathematische Modellbildung und Simulation in der Praxis, Partielle Differentialgleichungen, das Projektorientierte Praktikum, Inverse Probleme und Paralleles Rechnen. Anschließend stand die Vorbereitung der Masterarbeit zum Thema Mischung von nichtnewtonschen Fluiden im Vordergrund. Nichtnewtonsche Fluide finden sich überall, z.B. auch in der Medizin (hier vor allem das Fluid Blut). Seine Professor in Prag hat schon lange Beziehung zum Institut für experimentelle Medizin, deshalb war dieses Thema für beide Seiten (Karlsruhe und Prag) sehr interessant. Seine Vorkenntnisse und der Wunsch, die deutschen Sprache wirklich zu sprechen, erwiesen sich als Vorteil, weil Vojtěch Cvrček so leichter Kontakte knüpfen konnte zu den deutschen Studierenden und Mitarbeitern. Nach einer Anfangszeit mit einer Unterkunft am Stadtrand von Karlsruhe konnte er im Studentenwohnheim HaDiKo (kurz für Hans-Dickmann-Kolleg) einziehen, was einem reichhaltiges sozialen Leben zur Folge hatte und auch vielen Kontakten zu nicht-Mathematikern. Nach erfolgreichem Abschluss des Studiums in Prag wollte er gern in Deutschland eine Arbeit als Ingenieur finden. Dafür hat er auch die Karrieremessen des KIT genutzt, um direkt Kontakt zu Firmen zu knüpfen. Das hat schließlich dazu geführt, dass er sogar die Wahl zwischen verschiedenen Angeboten hatte. Er wird nun als Mathematiker im Maschinenbau tätig sein in der Nähe von Karlsruhe. Referenzen:
| |||||||||||||||||||
| 06 Oct 2016 | Robots | 00:20:36 | |||||||||||||||||
This is another conversation Gudrun had during the British Applied Mathematics Colloquium which took place 5th – 8th April 2016 in Oxford. Since 2002 Anette Hosoi has been Professor of Mechanical Engineering at MIT (in Cambridge, Massachusetts). She is also a member of the Mathematical Faculty at MIT. After undergraduate education in Princeton she changed to Chicago for a Master's and her PhD in physics. Anette Hosoi wanted to do fluid dynamics even before she had any course on that topic. Then she started to work as Assistant Professor at MIT where everyone wanted to build robots. So she had to find an intersection between fluid and roboters. Her first project were Robo-snailes with her student Brian Chan. Snails move using a thin film of fluid under their foot (and muscles). Since then she has been working on the fascinating boundary of flow and biomechanics. At the BAM Colloquium she was invited for a plenary lecture on "Marine Mammals and Fluid Rectifiers: The Hydrodynamics of Hairy Surfaces". It started with a video of Boston dynamics which showed the terrific abilities some human-like robots have today. Nevertheless, these robots are rigid systems with a finite number of degrees of freedom. Anette Hosoi is working in control and fluid mechanics and got interested in soft systems in the context of robots of a new type. Soft systems are a completely new way to construct robots and for that one has to rethink everything from the bottom up.You are a dreamer she was told for that more than once. For example Octopuses (and snails) move completely different to us and most animals the classcallly designed robots with two, four or more legs copy. At the moment the investigation of those motions is partially triggered by the plausible visualization in computer games and in animated movie sequences. A prominent example for that is the contribution of two mathematicians at UCLA to represent all interactions with snow in the animated movie Frozen. The short verison of their task was to get the physics right when snow falls off trees or people fall into snow - otherwise it just doesn't look right. To operate robots which are not built with mechanical devices but use properties of fluids to move one needs valves and pumps to control flow. They should be cheap and efficient and without any moving parts (since moving parts cause problems). A first famous example for such component is a fluid rectifier which was patented by Nicola Tesla in the 1920ies. His device relied on inertia. But in the small devices as necessary for the new robots there are no inertia. For that Anette Hosoi and her group need to implement new mechnisms. A promising effect is elasticity - especially in channels. Or putting hair on the boundary of channels. Hair can cause asymmetric behaviour in the system. In one direction it bends easily with the flow while in the opposite direction it might hinder flow. While trying to come up with clever ideas for the new type of robots the group found a topic which is present (almost) everywhere in biology - which means a gold mine for research and open questions. Of course hair is interacting with the flow and not just a rigid boundary and one has to admit that in real life applications the related flow area usually is not small (i.e. not negligible in modelling and computations). Mathematically spoken, the model needs a change in the results for the boundary layer. This is clear from the observations and the sought after applications. But it is clear from the mathematical model as well. At the moment they are able to treat the case of low Reynolds number and the linear Stokes equation which of course, is a simplification. But for that case the new boundary conditions are not too complicated and can be treated similar as for porous media (i.e. one has to find an effective permeability). Fortunately even analytic solutions could be calculated. As next steps it would be very interesting to model plunging hairy surfaces into fluids or withdrawing hairy surfaces from fluids (which is even more difficult). This would have a lot of interesting applications and a first question could be to find optimal hair arrangements. This would mean to copy tricks of bat tongues like people at Brown University are doing. References
| |||||||||||||||||||
| 05 Apr 2018 | Singular Pertubation | 00:21:57 | |||||||||||||||||
Gudrun had two podcast conversations at the FEniCS18 workshop in Oxford (21.-23. March 2018). FEniCS is an open source computing platform for solving partial differential equations with Finite Element methods. This is the first of the two episodes from Oxford in 2018. Roisin Hill works at the National University of Ireland in Galway on the west coast of Ireland. The university has 19.000 students and 2.000 staff. Roisin is a PhD student in Numerical Analysis at the School of Mathematics, Statistics & Applied Mathematics. Gudrun met her at her poster about Balanced norms and mesh generation for singularly perturbed reaction-diffusion problems. This is a collaboration with Niall Madden who is her supervisor in Galway. The name of the poster refers to three topics which are interlinked in their research. Firstly, water flow is modelled as a singularly perturbed equation in a one-dimensional channel. Due to the fact that at the fluid does not move at the boundary there has to be a boundary layer in which the flow properties change. This might occur very rapidly. So, the second topic is that depending on the boundary layer the problem is singularly perturbed and in the limit it is even ill-posed. When solving this equation numerically, it would be best, to have a fine mesh at places where the error is large. Roisin uses a posteriori information to see where the largest errors occur and changes the mesh accordingly. To choose the best norm for errors is the third topic in the mix and strongly depends on the type of singularity. More precisely as their prototypical test case they look for u(x) as the numerical solution of the problem for given functions b(x) and f(x). It is singularly perturbed in the sense that the positive real parameter ε may be arbitrarily small. If we formally set ε = 0, then it is ill-posed. The numercial schemes of choice are finite element methods - implemented in FEniCS with linear and quadratic elements. The numerical solution and its generalisations to higher-dimensional problems, and to the closely related convection-diffusion problem, presents numerous mathematical and computational challenges, particularly as ε → 0. The development of algorithms for robust solution is the subject of intense mathematical investigation. Here “robust” means two things:
In order to measure the error, the energy norm sounds like a good basis - but as ε^2 → 0 the norm → 0 with order ε . They were looking for an alternative which they found in the literature as the so-called balanced norm. That remains O(1) as ε → 0. Therefore, it turns out that the balanced norm is indeed a better basis for error measurement. After she finished school Roisin became an accountant. She believed what she was told: if you are good at mathematics, accountancy is the right career. Later her daughter became ill and had to be partially schooled at home. This was the moment when Roisin first encountered applied mathematics and fell in love with the topic. Inspired by her daughter - who did a degree in general science specialising in applied mathematics - Roisin studied mathematics and is a PhD student now (since Sept. 2017). Her enthusiasm has created impressive results: She won a prestigious Postgraduate Scholarship from the Irish Research Council for her four year PhD program. References
Podcasts
| |||||||||||||||||||
| 12 Apr 2018 | Wasserstofftankstellen | 00:46:56 | |||||||||||||||||
Gudrun unterhielt sich mit Meike Juliane Amtenbrink. Frau Amtenbrink hat von September 2017 bis Februar 2018 am Fraunhofer Institut für Solare Energiesysteme (ISE) in Freiburg Wasserstofftankstellen modelliert. Die Niederschrift der Ergebnisse bilden ihre Masterarbeit im Studiengang Energietechnik am KIT . Gudrun hat die Arbeit von Seiten des KIT als Erstgutachterin betreut. Als kohlenstofffreier Energieträger ist Wasserstoff im weltweiten Fokus der Forschung. Tanken mit Wasserstoff verspricht, den CO2-Ausstoß des Verkehrssektors zu reduzieren, zusätzlich ermöglicht die Umwandlung überschüssiger Strommengen in Wasserstoff mittels Elektrolyse dringend benötigte Flexibilität für die zukünftige Energieversorgung. Dafür müssen Tankstellen zur Verfügung stehen. Auf dem noch jungen Markt hat sich auf der Kundenseite bereits ein Standard etabliert, sodass alle Besitzerinnen eines Brennstoffzellenfahrzeugs an jeder Wasserstofftankstelle nachtanken können. Der technische Aufbau der Tankstellentechnologie ist dabei, je nach Anwendung, unterschiedlich. Teil der Arbeit war es einzuschätzen, welche Konzepte für den zukünftigen Markt eine Rolle spielen. Aufgrund der Vergleichbarkeit zwischen den relevanten Konzepten und dem in der ISE-eigenen Tankstelle umgesetzten Aufbau, wurde die institutseigene Tankstelle modelliert und die vorhandenen Messdaten genutzt, um die Plausibilität der Ergebnisse zu überprüfen. Im Rahmen vorangegangener Abschlussarbeiten wurde am Fraunhofer ISE ein Simulationsmodell eines Power-to-Gas-Systems auf Basis der PEM-Elektrolyse erstellt. Dieses Modell hatte zum Ziel, das dynamische Systemverhalten nachzubilden, Aussagen/Vorhersagen zum realen Wirkungsgrad der Anlage zu geben und die tatsächliche jährliche Wasserstofferzeugung zu prognostizieren. Darauf konnte Frau Amtenbrink aufbauen. In ihrer Arbeit wurde ein nulldimensionales, thermodynamisches Realgasmodell einer Wasserstofftankstelle in MATLAB/Simulink erstellt. Dafür wurden für die Einzelkomponenten einer Wasserstofftankstelle die Enthalpie- und Stoffbilanzen aufgestellt, in Simulink implementiert und über eine Steuerungslogik zu einem Gesamtsystem verbunden. Mit dem Tankstellenmodell können das Stand-by-Verhalten der Tankstelle und der Betankungsvorgang sekundengenau simuliert werden. Ergebnis sind die Drücke, Temperaturen und Stoffströme des Wasserstoffs an den relevanten Stellen im Gesamtsystem und der Energieverbrauch der Tankstelle, aufgeschlüsselt nach den wichtigsten Einzelkomponenten. Das Speichermodell kann auf Grundlage der Erhaltungsgleichungen über die zu- und abfließenden Stoffströme den sich ergebenden Druck und die Temperatur des Wasserstoffs im Speicher nachbilden, wobei die Realgasgleichung nach Redlich und Kwong benutzt wurde. Der Wärmeaustausch mit der Umgebung durch Konvektion und Wärmeleitung ist berücksichtigt. Das Modell ist auf verschiedene Speicher parametrisierbar und kann über die Anpassung der Geometrie- und Materialwerte sowohl für die Druckbänke an der Tankstelle, als auch für den Fahrzeugtank genutzt werden. Die Speichermodelle zeigen eine sehr gute Übereinstimmung mit der Realität. Die Drücke in Abhängigkeit der Umgebungstemperatur und die Temperaturerhöhung, die sich als Resultat einer Speicherbefüllung ergibt, können nachgebildet werden, ebenso der nach einer Befüllung erfolgende Temperaturausgleich mit Druckreduzierung. Durch das Modell für die Rohrleitungen können die Druckverluste innerhalb der Tankstelle abgebildet werden. Das Modell ist durch die Wahl der Geometrieparameter auf unterschiedliche Tankstellenkonfigurationen anwendbar. Der Kompressor wurde isentrop modelliert und die Verdichtungsarbeit mit einem isentropen Wirkungsgrad korrigiert. Der Druckanstieg, der sich durch den Kompressor beim Wiederbefüllen der Druckbank ergibt, ist durch die Simulation genau wiedergegeben. Dadurch ergibt sich, dass die Dauer der Speicherbefüllung zwischen Simulation und Messung übereinstimmt. Zur Modellierung der Kältemaschine wurde der Kältemittelkreislauf stark vereinfacht und durch eine Kälteleistung ersetzt, die von der Umgebungstemperatur abhängt. Für die wichtigsten Energieverbraucher an der Tankstelle, Kompressor und Kältemaschine, wurden Modelle erstellt, durch die der Energieverbrauch in Abhängigkeit der Betriebsführung berechnet werden kann. Nach der anschließenden Validierung kann das Modell dazu dienen, die Hauptenergieverbräuche an der Tankstelle zu quantifizieren und die Größe der einzelnen Komponeten optimal aufeinander auszulegen. Damit kann in Zukunft entschieden werden, ob zum Beispiel die Betriebsführung der Kältemaschine zur Optimierung des Gesamtwirkungsgrades verändert werden sollte. Literatur und weiterführende Informationen
Podcasts
| |||||||||||||||||||
| 19 Apr 2018 | Zweiphasenströmungen | 00:45:47 | |||||||||||||||||
Gudrun hatte zwei Podcast-Gespräche beim FEniCS18 Workshop in Oxford (21.-23. März 2018). FEniCS ist eine Open-Source-Plattform zur Lösung partieller Differentialgleichungen mit Finite-Elemente-Methoden. Dies ist die zweite der beiden 2018er Folgen aus Oxford. Susanne Claus ist zur Zeit NRN Early Career Personal Research Fellow an der Cardiff University in Wales. Sie hat sich schon immer für Mathematik, Physik, Informatik und Ingenieursthemen interesseirt und diese Interessen in einem Studium der Technomathematik in Kaiserlautern verbunden. Mit dem Vordiplom in der Tasche entschied sie sich für einen einjährigen Aufenthalt an der Universität Kyoto. Sie war dort ein Research exchange student und hat neben der Teilnahme an Vorlesungen vor allem eine Forschungsarbeit zu Verdunstungsprozessen geschrieben. Damit waren die Weichen in Richtung Strömungsrechnung gestellt. Dieses Interesse vertiefte sie im Hauptstudium (bis zum Diplom) an der Uni in Bonn, wo sie auch als studentische Hilfskraft in der Numerik mitarbeitete. Die dabei erwachte Begeisterung für nicht-Newtonsche Fluid-Modelle führte sie schließlich für die Promotion nach Cardiff. Dort werden schon in langer Tradition sogenannte viskoelastische Stoffe untersucht - das ist eine spezielle Klasse von nicht-Newtonschem Fluiden. Nach der Promotion arbeitet sie einige Zeit als Postdoc in London am University College London (kurz: UCL) zu Fehleranalyse für Finite Elemente Verfahren (*). Bis sie mit einer selbst eingeworbenen Fellowship in der Tasche wieder nach Cardiff zurückkehren konnte. Im Moment beschäftigt sich Susanne vor allem mit Zweiphasenströmungen. In realen Strömungsprozessen liegen eigentlich immer mindestens zwei Phasen vor: z.B. Luft und Wasser. Das ist der Fall wenn wir den Wasserhahn aufdrehen oder die Strömung eines Flusses beobachten. Sehr häufig werden solche Prozesse vereinfacht modelliert, indem man sich nur eine Phase, nämlich die des Wassers genau ansieht und die andere als nicht so wichtig weglässt. In der Modellbildung für Probleme, in denen beide Phasen betrachtet werden sollen, ist das erste Problem, dass das physikalische Verhalten der beiden Phasen sehr unterschiedlich ist, d.h. man braucht in der Regel zwei sehr unterschiedliche Modelle. Hinzu treten dann noch komplexe Vorgänge auf der Grenzflächen auf z.B. in der Wechselwirkung der Phasen. Wo die Grenzfläche zu jedem Zeitpunkt verläuft, ist selbst Teil der Lösung des Problems. Noch interessanter aber auch besonders schwierig wird es, wenn auf der Grenzfläche Tenside wirken (engl. surfactant) - das sind Chemikalien die auch die Geometrie der Grenzfläche verändern, weil sie Einfluß auf die Oberflächenspannung nehmen. Ein Zwischenschritt ist es, wenn man nur eine Phase betrachtet, aber im Fließprozess eine freie Oberfläche erlaubt. Die Entwicklung dieser Oberfläche über die Zeit wird oft über die Minimierung von Oberflächenspannung modelliert und hängt deshalb u.a. mit der Krümmung der Fläche zusammen. D.h. man braucht im Modell lokale Informationen über zweite Ableitungen. In der numerischen Bearbeitung des Prozesses benutzt Susanne das FEniCS Framework. Das hat sie auch konkret dieses Jahr nach Oxford zum Workshop geführt. Ihr Ansatz ist es, das Rechengitter um genug Knoten anzureichern, so dass Sprünge dargestellt werden können ohne eine zu hohe Auflösung insgesamt zu verursachen. (*) an der UCL arbeitet auch Helen Wilson zu viscoelastischen Strömungen, mit der Gudrun 2016 in Oxford gesprochen hat. Literatur und weiterführende Informationen
Podcasts
| |||||||||||||||||||
| 26 Apr 2018 | CAMMP | 00:35:33 | |||||||||||||||||
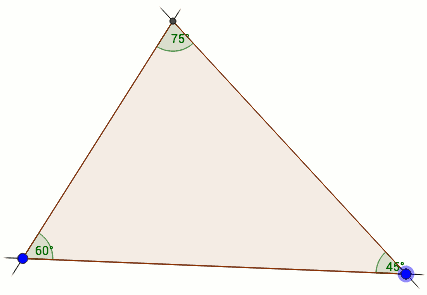
Gudrun hat sich mit Kirsten Wohak unterhalten. Sie ist seit Januar 2018 in der Arbeitsgruppe Computational Science and Mathematical Methods von Prof. Frank tätig. Diese Gruppe schlägt eine Brücke zwischen dem Steinbuch Center for Computing und der KIT-Fakultät für Mathematik. Thema des Gespräches war jedoch ein ganz besonderes Angebot für Schülerinnen und Schüler: Das Computational and Mathematical Modeling Program (CAMMP) . Zusammen mit Maren Hattebuhr kümmert sie sich um das schon an der RWTH Aachen erprobte Konzept nun auch in Karlsruhe. Beantwortet wird die Frage: Wie funktionieren eigentlich...
... und was hat das mit Mathe zu tun? Anhand solchen praxisorientierter Fragestellungen aus dem eigenen Alltag werden Schüler und Schülerinnen in die Grundlagen der mathematischen Modellierung eingeführt. Dabei finden mathematische Inhalte, wie beispielsweise Winkelsätze oder Matrizenrechnung Anwendung, die bereits aus dem Unterricht bekannt sind. Neben inhaltlicher Arbeit werden in den Workshops vor allem prozessbezogene Kompetenzen gefördert. Das typische Format ist ein sogenannter CAMMP-day. Er findet jeweils am Schülerlabor Mathematik im Mathebau statt und wird auf Anfrage je nach Themenwahl mit Oberstufen- bzw. Mittelstufenkursen von ein bis zwei wissenschaftlichen Mitarbeitern/-innen durchgeführt. Seit dem 23. April 2018 läuft für sechs Montage der Schnupperkurs Mathematik zum Thema GPS und Navigation und am heutigen Girls' day findet der Shazam-Kurs statt. Podcasts
| |||||||||||||||||||
| 17 May 2018 | Computergrafik | 00:36:32 | |||||||||||||||||
Das Treffens des German Chapters of European Women in Mathematics fand am 3. und 4. Mai 2018 im Mathematikon in Heidelberg statt. Am Rande der Konferenz der Mathematikerinnen sprach Gudrun mit Susanne Krömker. Sie leitet seit 2004 die Computergrafik-Gruppe des Interdisziplinären Zentrums für Wissenschaftliches Rechnen(IWR) an der Ruprecht-Karls-Universität Heidelberg. In der Computergrafik geht es grob gesagt um Analyse und Bearbeitung von Daten und ihre Darstellung als visuelle Information, d.h. es kommen sehr viele unterschiedliche Anforderungen zusammen. Andererseits sind die Themen, die jeweils dahinter stecken auch ganz besonders vielgestaltig. Für Susanne begann 1989 die Faszination mit der Darstellung einer reaktiven Strömung, bei der explosionsartig Wärme freigesetzt wird. Im Experiment ist die Apparatur geborsten, die Simulation liefert die Erklärung durch eine von den Wänden reflektierte Druckwelle und die Visualisierung macht den zeitlich enorm kurzen Explosionsvorgang mit Temperatur- und Druckverteilung im reaktiven Gemisch anschaulich.
Anschließend hat sie sich in ihrer Promotion mit partiellen Differentialgleichungen zur Beschreibung katalytischer Prozesse an Oberflächen beschäftigt, sich aber nie ganz von dem Thema Computergrafik getrennt, das in den 1990er Jahren dann richtig Fahrt aufnahm. Heute ist die Computergrafik technisch gesehen eine typische Anwendung für Hochleistungsrechnen. Außerdem gibt es immer wieder interessante Entwicklungen, die die Möglichkeiten von Grafikkarten unkonventionell ausnutzen. Aber es geht auch darum, geeignete Methoden zu entwicklen und zu implementieren, mit denen die von 3D-Scannern erfassten Messdaten auf ihren Informationsgehalt reduziert werden können. Grundsätzlich müssen dabei immer dreidimensionale Vorgänge auf dem zweidimensionalen Bildschirm dargestellt werden. Dazu braucht man projektive Geometrie - ein Thema, das in der Vorlesung mitunter abstrakt und von der Realität weit entfernt scheint. In ihrer Geometrie-Vorlesung für Sudierende der Mathematik kann Susanne ihre Erfahrungen aus der Informatik sehr anschaulich einbringen wie hier im Video für die Fano Ebene: (YouTube) Etwa seit dem Jahr 2000 gab es in der Arbeitsgruppe von Susanne viele besonders interessante und sehr unterschiedliche Projekte. Ein Forschungsschwerpunkt lag dabei in der Kombination von Computertomographie und Oberflächendaten, um aus beiden Bildgebungsverfahren im Resultat ein verbessertes Bild zu erhalten: ILATO-Projekt (Improving Limited Angle computed Tomography by Optical data integration). Außerdem hat sich die enge Zusammenarbeit mit Archäologen, Historikern und Geologen als besonders fruchtbar erwiesen. Beispiele dafür sind der theoriebildende Diskurs zum digitalen Modell des Klosters Lorsch (seit 1991 Weltkulturerbe der UNESCO) oder die Rekonstruktion von Inschriften in Tafeln und auf Grabsteinen, z.B. auf dem jüdischen Friedhof in Worms. Diese Analyse basiert auf Multiskalen Integralinvarianten, einem Filterverfahren, das in dem Softwareframework GigaMesh (Autor: Hubert Mara, IWR, Universität Heidelberg) implementiert ist. Oder die Rekonstruktion der Karten von barocken Globen, u.a. des Gottorfer Globus, mit HiIfe von anisotrop diffusiver Filterung. Die Arbeitsgruppe hat Ausgrabungen im Tempelgebiet von Angkor in Kambodscha, dem größten Tempelgebiet der Welt, wissenschaftlich begleitet. Es gelang eine virtuelle architektonische Rekonstruktion des größten Tempels Angkor Wat oder die Rekonstruktion einer sechs Meter hohen Schiva-Statue aus Koh Ker, von der einzelne Puzzle-Teile über mehrere Museen der Welt verstreut sind. Susanne hatte sich 1983 zunächst für ein Studium der Mathematik und Betriebswirtschaft in Osnabrück entschieden, hat dann aber den Wechsel nach Heidelberg verbunden mit der Hinwendungen zu anderen Natur- und Geisteswissenschaften nie bereut. Literatur und weiterführende Informationen
| |||||||||||||||||||
| 03 Oct 2013 | Mathematische Modellbildung | 00:37:21 | |||||||||||||||||
Gudrun Thäter spricht mit Sebastian Ritterbusch über Mathematische Modellbildung und die zugehörige Vorlesung im Studium, über überraschende Ventile, dem Stau aus dem Nichts und Fußgängersimulationen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 10 Oct 2013 | Die Aorta-Challenge | 00:36:08 | |||||||||||||||||
Thomas Henn spricht mit Sebastian Ritterbusch über seine Blutflusssimulationen in der Aorta, die mathematische Beschreibung, wie man über ein Becken geht, numerische Simulationen auf einem Großrechner und über den internationalen Vergleich der Ergebnisse. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 17 Oct 2013 | Unsichtbarkeit | 00:42:23 | |||||||||||||||||
Andreas Helfrich-Schkarbanenko befasst sich mit der mathematischen Beschreibung der Unsichtbarkeit, Metamaterialien und berichtet im Gespräch mit Sebastian Ritterbusch über Simulationsexperimente zu akustischen und elektromagnetischen Tarnkappen. Zusammen mit Muamer Kadic und Philipp Klas passten sie eine Tarnkappe an ein inhomogenes Hintergrundmedium an. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 24 Oct 2013 | Erdölsuche | 01:00:49 | |||||||||||||||||
Jörg Bäuerle hat ein Verfahren zur verbesserten Erdölsuche erforscht, das passiv die elektromagnetische Ausstrahlung von Erdölfeldern auswerten kann. Wie im Gespräch mit Sebastian Ritterbusch zu hören, steckt darin viel Mathematik, Freude über L-Kurven und nicht nur ein inverses Problem. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 31 Oct 2013 | Pumpspeicherkraftwerke | 00:42:44 | |||||||||||||||||
Julia Dickmann optimiert den Betrieb von Pumpspeicherkraftwerken ohne die Zukunft der Strompreise und Regenfälle genau zu kennen. Dazu geht sie im Gespräch mit Sebastian Ritterbusch auf Zeitreise aus der Zukunft in die Gegenwart, und berechnet so mit Topologiematrix und Simplex-Verfahren optimale Steuerungsstrategien auf Basis von statistischen Modellen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 07 Nov 2013 | Computertomographie | 00:35:38 | |||||||||||||||||
Yuemin Liang hat Methoden entwickelt, mit denen Bewegungen während einer Computertomographie herausgerechnet werden können, um bessere Rekonstruktionen zu erhalten. Dafür verwendet sie Marker, die im Sinogramm verräterische Spuren zeigen, wenn es zu Bewegungen gekommen ist, kann so die ungewollten Bewegungen zum Teil kompensieren, und erklärt das Ganze im Gespräch mit Sebastian Ritterbusch. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 14 Nov 2013 | Ad-hoc Netzwerke | 01:01:14 | |||||||||||||||||
Leonid Chaichenets hat Ad-hoc Netze modelliert, und dadurch die Optimierung der erfolgreichen Übertragungen ermöglicht. Er erklärt im Gespräch mit Sebastian Ritterbusch wie mit Verfahren aus der stochastischen Geometrie in Zukunft bessere Kommunikationsnetze für Notkräfte entwickelt werden können. Ein besonderes Merkmal der Netze ist, dass einzelne Teilnehmer nichts über ihre Kommunikationspartner wissen. Wie soll es funktionieren, dass nicht alle versuchen gleichzeitig zu senden? Mit einer geschickten Aloha Strategie kann man alleine aus dem Verhalten der Teilnehmer die Qualität des Netzes im Voraus berechnen und damit die Gesamtleistung optimieren. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 21 Nov 2013 | Injektoren | 00:29:17 | |||||||||||||||||
Carmen Straub modelliert und simuliert den Einspritzvorgang im Motorraum durch Injektoren. Dabei hat sie das Modell und die numerischen Verfahren auf Stabilität untersucht indem sie numerische Lösungen mit einer analytischen Lösung verglich. Um den Einsatz neuer Forschungsergebnisse um Large-Eddy-Simulationen zu untersuchen hat sie das Modell mit einem neuen Softwarepaket gekoppelt. Diese Ergebnisse wurden mit einem echten Einspritzvorgang verglichen. Dabei hat sie auch viel mit Ingenieuren in Deutschland und USA zusammengearbeitet und Forschung in der Industrie kennengelernt, und erzählt uns davon im Gespräch mit Gudrun Thäter. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 05 Dec 2013 | Positionsbestimmung | 00:35:17 | |||||||||||||||||
Hakan Demirel hat die Positionsbestimmung auf der Erde untersucht, wie sie zum Beispiel mit dem Global Positioning System möglich ist. Dabei geht er im Gespräch mit Gudrun Thäter auch auf Fehlerquellen ein, die auf sehr unterschiedliche Arten, die bestimmte Position verfälschen können, und wie Blitze verortet werden können. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 12 Dec 2013 | Flammen | 00:18:13 | |||||||||||||||||
Auch Flammen können durch partielle Differentialgleichungen modelliert werden, und Robin Trunk hat so ein Modell mit Hilfe von Level-Set Methoden numerisch mit Finiten Elementen simuliert. Im Gespräch mit Gudrun Thäter geht er auch auf die Zusammenarbeit mit den Ingenieuren am IKET und das Studium der Technomathematik ein. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 19 Dec 2013 | Erdbeben | 00:37:57 | |||||||||||||||||
Erdbeben lassen sich nicht verhindern, doch wir lernen immer besser mit ihnen umzugehen. Dafür simuliert Stephanie Wollherr die Erdschwingungen und erklärt im Gespräch mit Gudrun Thäter, wie wir mit optimaler Versuchsplanung bessere Aufstellorte für Seismographen bestimmen können. Durch das Modell in schwacher Formulierung und Optimierung des Messnetzes mit Fisher-Informationsmatrix erhalten wir ein genaueres Bild über die physikalischen Vorgänge in der Erde und letztlich eine bessere Grundlage für Vorhersagen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 09 Jan 2014 | Strömungssteuerung und Gebietszerlegung | 00:20:10 | |||||||||||||||||
Luftströmungen sorgen für den Auftrieb von Flugzeugen, und sind zu großem Teil durch den Luftwiderstand für den Treibstoffverbrauch im Auto verantwortlich. Deswegen untersucht Eva Ketelaer, wie man mit Finiten Elementen Strömungen simulieren und optimal steuern kann, und erläutert im Gespräch mit Gudrun Thäter auch, wie man die Verfahren auch auf Hochleistungsrechner mit Zerlegungsmethoden skalieren kann. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 30 Jan 2014 | Windsimulation im Stadtgebiet | 00:46:41 | |||||||||||||||||
Irina Waltschläger modelliert den Wind im Stadtgebiet, um die Luftbewegung ausgehend von einem Gebäude- und Geländemodell mit den Navier-Stokes Gleichungen als Fluid simulieren und analysieren zu können. Im Gespräch mit Sebastian Ritterbusch erklärt sie, wie sie dazu künstliche Randbedingungen auf der Basis meteorologischer Erkenntnisse zum Windprofil entworfen hat, und deren Einfluss auf die Simulation analysierte. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 06 Feb 2014 | Lawinen | 00:16:36 | |||||||||||||||||
Lawinen und Muren sind im alpinen Bergland allgegenwärtige Gefahren, daher ist die Simulation des Abgangs gerade für Anwohner und Versicherungen sehr wichtig. Auf Basis eines Geländemodell aus dem Grass GIS Geoinformationssystem hat Katharina Schratz das mathematische Modell numerisch umgesetzt, und geht im Gespräch mit Sebastian Ritterbusch auf die Besonderheiten der Diskretisierung und der speziellen CFL-Bedingungung für numerische Stabilität ein. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 13 Feb 2014 | Lärmschutz | 00:32:08 | |||||||||||||||||
Der Autoverkehr macht Lärm, und vor diesem möchte man die Umwelt mit Lärmschutzwänden oder Lärmschutzwällen schützen. Tilo Arens erklärt im Gespräch mit Sebastian Ritterbusch, wie man die Schallausbreitung mit der Helmholtz-Gleichung mathematisch modellieren kann und durch das Huygens-Prinzip mit Randelementen und Integralgleichungen simulieren kann. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 20 Feb 2014 | Migräne | 01:54:51 | |||||||||||||||||
Das Gehirn ist nicht nur eine graue Substanz, sondern ein sehr komplexes Organ, wo es noch viel zu erforschen gibt. Markus Dahlem befasst sich mit der Migräne, und erklärt im Gespräch mit Gudrun Thäter und Sebastian Ritterbusch, wie hier mit Modellbildung im Gehirn neue Erkenntnisse erzielt werden: Migräne ≠ Kopfschmerzen, auf diese einfache Formel kann man es bringen. Denn Migräne ist eine Krankheit, Kopfschmerz ein Symptom. Kopfschmerzen sind nicht einmal notwendiges Merkmal dieser Volkskrankheit, die, je nach Detailtiefe der Diagnose, in bis zu 19 Unterformen klassifiziert werden kann, eine davon ohne Kopfschmerzen dafür mit visuellen Halluzinationen, die man Aura nennt. Laut der neusten Studie der Weltgesundheitsorganisation über die globale Gesundheitsbelastung ist Migräne weltweit für fast 3% der Behinderungen verantwortlich. Damit befindet sich Migräne an achter Stelle der am schwersten belastenden Krankheiten und auf dem ersten Platz unter den neurologischen Erkrankungen. Wie kann hier die Mathematik helfen? Der Verlauf einer Migräne mit Aura ist kennzeichnend für einen bestimmten Mechanismus raum-zeitlicher Strukturen. Solche Strukturen zum Beispiel in Form lokalisierter Wellensegmente sind in der Musterbildung aus Reaktion-Diffusions-Systemen vom Aktivator-Inhibitor-Typ bekannt. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 27 Feb 2014 | Sicherheitsventile | 00:22:53 | |||||||||||||||||
Sicherheitsventile sollen uns durch eine geeignete Auslegung vor Explosionen und Unglücken wie dem Sevesounglück in der Industrie schützen. Doch sind die aktuellen Sicherheitsrichtlinien zeitgemäß? Andreas Schleich hat dazu ein Sicherheitsventil mathematisch modelliert und mit der Lattice-Boltzmann Methode den Betrieb mit numerischer Fluid-Simulation simuliert. Dazu verwendete er ein Large-Eddy Modell zur Turbulenzmodellierung und validierte die Methode mit dem Strömungswiderstandskoeffizient (cW-Wert) einer Metallkugel. Im Gespräch mit Sebastian Ritterbusch erzählt er auch über Vakuumbläschen und andere Herausforderungen in der Simulation. Literatur und Zusatzinformationen
| |||||||||||||||||||
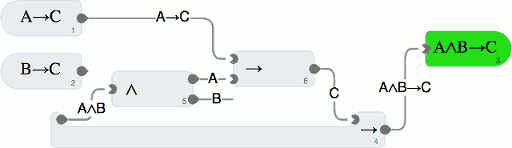
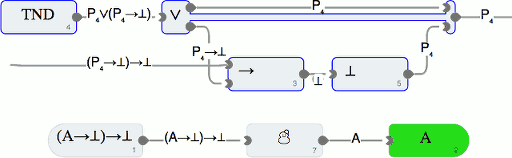
| 17 Apr 2014 | Computerunterstütztes Beweisen | 00:40:30 | |||||||||||||||||
Dagmar Rütters führt im Gespräch mit Gudrun Thäter die Technik ein, Computer unterstützte Beweise zu führen. Eine große Rolle spielt hierbei eine mathematisch korrekte Berechnung aller Größen, die zum Beispiel durch Intervallarithmetik möglich wird . Literatur und Zusatzinformationen
| |||||||||||||||||||
| 24 Apr 2014 | Zeitreihen | 00:32:50 | |||||||||||||||||
Zeitreihen erleben wir bei Aktienkursen, seismischen Messungen, Wetterbeobachtungen, Wahlen und vielem mehr. Franziska Lindner befasst sich deshalb mit der Zeitreihenanalyse und wie man mit mathematischen Methoden und Statistik Aussagen über die Struktur der Zeitreihen, Ereignisse im Zeitverlauf und Prognosen mit Konfidenzbereichen bestimmen kann. Im Gespräch mit Gudrun Thäter erläutert sie das Prinzip der Stationarität und den Einsatz der Fourieranalyse und das statistische Resampling in der Zeitreihenanalyse. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 15 May 2014 | Chromatographie | 00:49:25 | |||||||||||||||||
Tobias Hahn simuliert mit einem Konvektions-Diffusions-Modell die Makrokinetik in einer Chromatographie-Säule zur Isolation und Analyse von Proteinen und Antikörper für verbesserte Medikamente und viele weitere bio-chemische Produkte. Im Gespräch mit Gudrun Thäter erklärt er, wie Simulationen die Chromatographie verbessern und die Anzahl von Experimenten verringern. Eine besonders wichtige Anwendung ist auch die Parameterschätzung von unbekannten Größen aus durchgeführten Experimenten, wo durch das Fitting der Simulation an die gemessenen Daten die einzelnen Prozesse analysiert werden können. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 22 May 2014 | Versuchsplanung | 00:31:26 | |||||||||||||||||
Mit Differentialgleichungsmodellen werden oft zeitliche und/oder räumliche Prozesse modelliert, beispielsweise auch enzymatisch katalysierte Reaktionen. Anna Osberghaus schildert im Gespräch mit Gudrun Thäter, wie sie in ihrer Diplomarbeit mit Hilfe von Modelldiskriminierung unter den möglichen Reaktionswegen eines bestimmten Enzyms den wahrscheinlichsten bestimmt hat und danach mittels optimaler Versuchsplanung Experimente entworfen hat, die die Entscheidung für einen bestimmten Reaktionsweg in Zukunft vereinfachen sollten. Nebenbei schildert sie humorvoll und ehrlich ihren Werdegang von einer an "echten Daten" interessierten Mathematikstudentin zum PostDoc im Ingenieurwesen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 05 Jun 2014 | Gasspeicher | 00:40:15 | |||||||||||||||||
Um Gasspeicher mit möglichst viel Gewinn zu betreiben, verwendet Viola Riess Markov-Prozesse, um mit statistischen Methoden und durch mathematische Modelle optimale Handelsstrategien zu berechnen. Dabei muss sie neben Vorhersagemodellen für den Gaspreis auch die Restriktionen des Speichers in Füllstand und Kapazität berücksichtigen. Im Gespräch mit Gudrun Thäter erklärt sie die Diskretisierung des stochastischen Prozesses in ein Gitter, und die Rückwärtsinduktion zur Bewertung der Strategie, wie wir sie auch schon im Podcast zu Pumpspeicherkraftwerken kennengelernt hatten. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 12 Jun 2014 | Wasserstraßen | 00:35:10 | |||||||||||||||||
An der Bundesanstalt für Wasserbau (BAW) befasst sich Rebekka Kopmann in der Abteilung für Flusssysteme mit Analysen und Prognosen des Systemzustands von Bundeswasserstraßen. Strömungsmodelle liegen am BAW sowohl als nachgebaute Modelle von Flussstücken als auch als mathematisch beschriebene Computermodelle vor, die nur im Rechner simuliert werden. Im Gespräch mit Gudrun Thäter beschreibt sie die Herausforderung der Kalibration der Simulationsmodelle an die Wirklichkeit, damit sinnvolle Analysen und Prognosen möglich werden. Neben vielen weiteren Parametern ist die Rauheit im Fluss sehr wichtig und ist leider nur sehr zeitaufwendig zu bestimmen. Die Aufgabe führt sie auf ein Optimierungsproblem zurück, wo die unbekannten Parameter durch Annäherung vielfach ausgeführter Simulationen an die gemessene Wirklichkeit bestimmt werden. Da eine einzelne Flusssimulation teilweise tagelang rechnet, sucht sie nach sinnvollen Vereinfachungen oder Alternativen, die das Problem schneller lösen. Aktuell werden Methoden der Automatischen Differentiation eingesetzt, die helfen Gradientenverfahren zur Annährung an die Lösung zu beschleunigen. Dabei trifft man auch auf interdisziplinäre Herausforderungen, wenn es um die feinen mathematischen Unterschiede zum Beispiel zwischen Ableitung, Steigung und einem Gradienten geht. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 26 Jun 2014 | Predictive Analytics | 00:32:45 | |||||||||||||||||
Bei Blue Yonder, einem führenden Lösungsanbieter im Bereich Prognosen und Mustererkennung in Europa, arbeitet Florian Wilhelm an verschiedenen Kundenprojekten und spricht darüber mit Gudrun Thäter. Ein konkretes Beispiel sind Absatzprognosen für einen Kunden im Einzelhandel. Mit diesen Prognosen kann der Disponent eine optimale Entscheidung treffen wie viele Produkte er von einem Großhändler kauft, um bei hoher Warenverfügbarkeit möglichst geringe Abschreibungen durch verdorbene Ware zu haben. Zur Generierung dieser Prognosen werden sowohl Methoden aus dem Bereich des Maschinellen Lernens wie auch der Statistik angewendet. Manche Methoden haben ihren Ursprung in der Teilchenphysik, wo sie verwendet werden um Teilchen in den Experimenten am CERN nachzuweisen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 03 Jul 2014 | Last-Call Auktionen | 00:18:45 | |||||||||||||||||
Last-Call Auktionen sind Auktionen, in denen ein Bieter bevorzugt wird. Marie-Christin Haufe beschäftigt sich in ihrer Diplomarbeit mit dieser Auktionsform und untersucht, wie sich die Vergabe eines Last-Call Rechts auf das Bietverhalten der nichtbevorzugten Bieter auswirkt. Dabei werden spieltheoretische Gleichgewichte berechnet, ökonomisch interpretiert und ihre Auswirkungen auf den erwarteten Auktionserlös mathematisch analysiert. Im Gespräch mit Gudrun Thäter erklärt sie, wie sie mit der Modellierung durch die Betaverteilung Aussagen über die Bieterstärken, Wertschätzung und der Aggressivität im Auktionsprozess sowohl als Erstpreisauktion als auch in einer Zweitpreisauktion treffen konnte. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 17 Jul 2014 | Wahlsysteme | 00:25:08 | |||||||||||||||||
Wahlsysteme definieren den Ablauf von Wahlen, und wie daraus ein Wahlergebnis bestimmt wird. Dieses Ergebnis soll die oft sehr unterschiedlichen Vorstellungen der Wählenden möglichst gut repräsentieren. Philipp Staudt hat dazu mathematisch analysiert, wie das deutsche Wahlsystem gegenüber alternativen Verfahren wie der Rangaddition und der Condorcet-Methode abschneidet. Ein besonderes Augenmerk lag im Gespräch mit Gudrun Thäter auch auf der Frage, wie die 5 Prozent-Klausel unter verschiedenen Voraussetzungen das Ergebnis beeinflusst. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 24 Jul 2014 | Getriebeauswahl | 00:25:33 | |||||||||||||||||
Getriebe sind mechanische Komponenten, die oft zwischen Motoren und anzutreibenden Maschinenteilen zum Einsatz kommen, und übersetzen Drehmomente und Drehzahlen. Für einen Anwendungsfall gibt es aber viele einsetzbare Getriebe mit vielen weiteren Eigenschaften, wie Wirkungsgrad, Geräuschentwicklung, Größe, Gewicht und vieles mehr. Jonathan Fröhlich hat hier die Frage betrachtet, wie man bei der Auswahl des Getriebes vorgehen kann, und erklärt im Gespräch mit Gudrun Thäter, wie hier der Analytic Hierarchy Process den Entscheidungsprozess durch die Berechnung von Eigenwerten und Eigenvektoren unterstützen kann. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 31 Jul 2014 | Unfallvorhersage | 00:27:02 | |||||||||||||||||
Aus einem Verkehrsmodell kann man den Straßenverkehr simulieren und damit mögliche Staustellen und auch die Gefahr für Verkehrsunfälle vorhersagen. Dafür wird das Straßennetz in ein Netzwerk aus Knoten und Kanten zerlegt, und mit stochastischen Methoden aus früheren Messungen Aussagen über die Zukunft getroffen und Auswirkung von Änderungen analysiert. Marianne Petersen hat dazu den Verkehr im Rhein-Main-Gebiet betrachtet und beschreibt im Gespräch mit Gudrun Thäter, wie sie mit Bayes-Verfahren, Regressionsanalyse und Poisson-Verteilungen gerade auch seltene Unfallereignisse analysieren konnte. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 07 Aug 2014 | Motorisches Lernen | 00:48:04 | |||||||||||||||||
Kinder erlernen das Laufen und Schreiben im Spiel, doch für Erwachsene ist es nach z.B. einem Schlaganfall eine ganz andere Herausforderung. Daher untersucht Christian Stockinger im BioMotion Center das motorische Lernen, damit wir besser verstehen können, wie sich der Körper sensormotorische Programme abruft. Mit einem Robotic Manipulandum, dem BioMotionBot, lässt er dazu die Probanden einfache Armbewegungen durchführen, die unbemerkt durch ein Kraftfeld gestört werden. Dadurch erlernen sie unbemerkt neue Bewegungsabläufe, und im Gespräch mit Gudrun Thäter erklärt er, wie man diesen Lernvorgang mathematisch mit einem Zwei-Prozessmodell beschreiben kann. Daraus kann man sowohl viel über die Vorgänge lernen, Therapien verbessern, als auch die Entwicklung von modernen Prothesen und humanuider Roboter voranbringen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 14 Aug 2014 | Matrixfunktionen | 00:25:04 | |||||||||||||||||
Eine Funktion, die eine Matrix auf eine Matrix abbilden kann, ist eine Matrixfunktion. Diese Funktionen finden besonders bei der numerischen Behandlung von Evolutionsgleichungen wie zum Beispiel der Wärmeleitungsgleichung ihre Anwendung. Dazu bändigt Tanja Göckler die komplizierten partiellen Differentialgleichungen, die aus der mathematischen Modellbildung entstehen, durch Diskretisierung und weiteren Methoden zu gewöhnlichen Differentialgleichungen. Diese können durch Potenzreihen gelöst werden, die auch als Matrixfunktionen eingesetzt werden können. So kann man beispielsweise auch die Exponentialfunktion als Potenzreihe auf eine Matrix anwenden, um lineare Differentialgleichungen zu lösen. Im Gespräch mit Gudrun Thäter erklärt sie, wie man diese Aufgaben aber mit rationalen Krylov-Verfahren noch viel effizienter lösen kann. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 21 Aug 2014 | Digitale Währungen | 02:22:18 | |||||||||||||||||
Um im digitalen Umfeld elektronischen Handel zu betreiben, benötigt man einen gesicherten Datenaustausch für Angebote, Verhandlungen und Verträge, aber letztlich auch eine Form von elektronischem Geld auf dem der Handel basiert. Ganz zentral ist dabei die moderne Kryptographie und insbesondere die Public Key-Verfahren, die durch mathematische Verfahren das ganze ermöglichen, soweit die Verfahren sicher, korrekt implementiert und richtig benutzt werden, und es nicht zu einem Fiasko wie dem Heartbleed-Bug kommt. Im Gespräch mit Gudrun Thäter erläutert Sebastian Ritterbusch die Mathematik hinter digitalem Geld und der Kryptowährung Bitcoin. Dazu geht es zunächst in die Zahlentheorie der Restklassenkörper Literatur und Zusatzinformationen
| |||||||||||||||||||
| 11 Sep 2014 | Logistik und Big Data | 00:14:10 | |||||||||||||||||
Im Bereich der Logistik geht es um die fortlaufende Optimierung des Geschäftsprozesses und dies kann man inzwischen auf Basis einer großen Menge von teilweise komplex strukturierten Echtzeitdaten, kurz gesagt Big Data, umsetzen. Liubov Osovtsova hat dazu ein Modell der Transportlogistik auf Basis von Petri-Netzen in CPN Tools in der Form eines Coloured Petri Net aufgestellt. Im Gespräch mit Gudrun Thaeter erklärt sie, wie sie damit unter Nutzung des Gesetz von Little und Warteschlagentheorie stochastische Aussagen über Engpässe und Optimierungspotentiale bestimmen konnte. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 18 Sep 2014 | Höhere Mathematik | 00:48:24 | |||||||||||||||||
Auch im Studium der Ingenieurswissenschaften steckt viel Mathematik: Diese spielt besonders am Anfang des Studiums der Fächer Maschinenbau, Verfahrenstechnik und Chemieingenieurwesen am KIT eine große Rolle, und Frank Hettlich begleitet mit seinem Team die Studienanfänger in der sogenannten Höheren Mathematik in den ersten drei Semestern. Dabei geht es ihm in den Vorlesungen nicht um die Vermittlung von Patentrezepten, sondern um den kreativen Umgang mit mathematischen Methoden, die für das weitere Studium eine große Rolle spielen werden.Um den Übergang von der Schulmathematik zur universitären Mathematik zu erleichtern, gibt es einen sehr gut besuchten zwei-wöchigen Vorkurs parallel zur Orientierungsphase vor dem eigentlichen Vorlesungsbeginn. Im Gespräch mit Gudrun Thäter erzählt er, dass es besonders wichtig ist, einfach den Stift wieder in die Hand zu nehmen und sich selbst an der Mathematik zu versuchen, um den Einstieg erfolgreich zu vollbringen. Dafür gibt es viele Übungen, anwendungsnahe Beispiele und Materialen, wie das Buch zur Mathematik, in das Frank Hettlich seine langjährigen Erfahrungen aus der Lehre einbringen konnte.Ganz wichtig ist es auch, die Begeisterung für das wissenschaftliche Vorgehen zu vermitteln, und die Studierenden zur Zusammenarbeit anzuregen. Letztlich gibt es aber auch Klausuren zur Mathematik, die zumindest in Karlsruhe eher weniger den Grund für einen Studienabbruch liefern. Keinesfalls sollten sie aber die leichte Schulter genommen werden, und auch dazu hat Frank Hettlich einige wichtige Tipps: Zeitplanung, Zusammenarbeit und Vorsicht im Umgang mit Lösungen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 16 Oct 2014 | Leistungsstrukturanalyse im Triathlon | 00:29:53 | |||||||||||||||||
Die wissenschaftliche Fundierung des sportlichen Trainings kann sowohl im Amateur- als auch im Profibereich zur Verbesserung der individuellen Leistung beitragen. Marian Hoffmann ist Mitarbeiter des BioMotion Centers und beschäftigt sich mit dem Einsatz multivariater Verfahren zur Identifikationen leistungsrelevanter Einflussgrößen durch Strukturgleichungsmodelle in der Sportart Triathlon. Hierzu zählen beispielsweise Kraft- und Ausdauerfähigkeiten sowie technische und taktische Merkmale. Im Gespräch mit Gudrun Thäter erläutert er den Einsatz mathematischer Methoden zur Bearbeitung dieser interdisziplinären Aufgabenstellung mit dem Ziel, spezifische Trainingsempfehlungen auf Basis einer Leistungsstrukturanalyse in dieser Ausdauersportart generieren zu können. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 06 Nov 2014 | Analysis und die Abschnittskontrolle | 02:13:59 | |||||||||||||||||
Im Herbst beginnen die neuen Studiengänge der Mathematik am KIT und neben den Vorlesungen zur Linearen Algebra, Stochastik oder Numerik gehört die Analysis zu den mathematischen Vorlesungen, mit dem das Studium der Mathematik in den ersten Semestern beginnt. Dazu spricht Sebastian Ritterbusch mit Johannes Eilinghoff, der im letzten Jahr den Übungsbetrieb der Analysis-Vorlesungen mit großem Anklang organisiert hat. Die Analysis befasst sich besonders mit der Mathematik um Funktionen auf reellen Zahlen, welche Eigenschaften sie haben, und wie man diese differenzieren oder integrieren kann. Vieles zur Geschichte der Analysis findet man besonders in den Büchern von Prof. Dr. Michael von Renteln, der unter anderem über die Geschichte der Analysis im 18. Jahrhundert von Euler bis Laplace, die Geschichte der Analysis im 19. Jahrhundert von Cauchy bis Cantor, über Aspekte zur Geschichte der Analysis im 20. Jahrhundert von Hilbert bis J. v. Neumann und über die Die Mathematiker an der Technischen Hochschule Karlsruhe 1825-1945 geschrieben hat. Grundlage für die Mathematik in der Analysis sind die Zahlenmengen, wie die abzählbaren natürlichen Zahlen Ein Beispiel für eine Folge rationaler Zahlen, die gegen eine irrationale Zahl konvergieren ist Über den Begriff der Folge kann man auch offene Mengen und abgeschlossene Mengen definieren, so wie dies auch mit Epsilon-Umgebungen definiert werden kann. Diese Eigenschaften werden im Bereich der mathematischen Topologie noch viel umfassender eingeführt, aber schon diese Darstellungen helfen, den wichtigen Begriff der Funktion in der Analysis und deren Eigenschaften einzuführen. Zur Definition einer Funktion gehört neben der eigentlichen Abbildungsvorschrift die Angabe der Definitionsmenge und der Wertebereich. Ohne diese Informationen ist es nicht möglich Surjektivität und Injektivität nachzuweisen. Eine wichtige Eigenschaft von Funktionen ist der Begriff der Stetigkeit, die man für den Zwischenwertsatz benötigt. Damit kann man zum Beispiel wackelnde Tische reparieren oder mit Anastasia im Science Slam Orte gleicher Temperaturen auf der Erde suchen. Der Zwischenwertsatz gilt zunächst nur für reelle Funktionen, es gibt den Zwischenwertsatz aber auch in allgemeinerer Form. Eine weitere wichtige Eigenschaft von Funktionen ist die Differenzierbarkeit und das Berechnen von Ableitungen mit ihren Ableitungsregeln. Sehr wichtig ist dabei die Exponentialfunktion, die mit ihrer eigenen Ableitung übereinstimmt. Diese Funktion findet man im Alltag in jeder Kettenlinie in der Form des Cosinus Hyperbolicus wieder. Eine wichtige Anwendung für differenzierbare Funktionen ist der Mittelwertsatz, ohne den die Abschnittskontrolle auf Autobahnen zur Geschwindigkeitsüberprüfung nicht denkbar wäre. Aber auch in höheren Dimensionen kann man Differentialrechnung betreiben, und man führt dazu den Gradienten, Richtungsableitungen und z.B. die Divergenz eines Vektorfelds ein. Als Umkehrung der Differentiation erhält man die Integralrechnung. Jedoch ist das Bilden einer Stammfunktion nur bis auf eine Konstante eindeutig. Daher kann man zum Beispiel mit Beschleunigungssensoren im Handy nicht wirklich eine Positions- und Geschwindigkeitsmessung durchführen, sondern muss für die Trägheitsnavigation viele weitere Sensoren mit einbeziehen. Eine andere Einführung des Integrals ist das Lebesgue-Integral oder das Riemannsche Integral, wo man bei letzterem in einem Intervall die Fläche unter einer Kurve durch Treppenfunktionen annähert. Den Zusammenhang dieser beiden Begriff liefert der Fundamentalsatz der Analysis. Leider kann man nicht zu allen Funktionen analytische Stammfunktionen bestimmen. Hier kann dann die numerische Integration zum Einsatz kommen. Die Integration ist aber keine rein abstrakte Idee, sondern wir finden mathematische Zusammenhänge wie den Gaußsche Integralsatz direkt in der Natur wieder. Für den Start im Studium erhält man in Karlsruhe viel Unterstützung: Es gibt Vorkurse und die von der Fachschaft für Mathematik und Informatik organisierte Orientierungsphase, oder kurz O-Phase, in der man die zukünftigen Mitstudierenden kennenlernen kann. Mit diesen sollte man sich gemeinsam den Stoff von Vorlesungen, Übungen und Tutorien erarbeiten, um sich mit gelösten Übungsblättern zur Klausteilnahme zu qualifizieren, und letztlich auch die Prüfungen gemeinsam vorzubereiten. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 13 Nov 2014 | Metallschaum | 01:39:52 | |||||||||||||||||
In den Materialwissenschaften ist man immer auf der Suche nach neuen Werkstoffen und Materialien. Sehr vielversprechend sind dabei Metallschäume, dessen Wärmeleitungseigenschaften Anastasia August am Institut für angewandte Materialien erforscht und über die sie uns im Gespräch mit Sebastian Ritterbusch erzählt. Zu den besonderen Eigenschaften von Metallschäumen gehören unter anderem die große Oberfläche bzw. Grenzfläche im Verhältnis zum Volumen wie bei Lungenbläschen und die hohe Wärmeleitungsfähigkeit im Verhältnis zum Gewicht. Gleichzeitig können Metallschäume mit Luft oder anderen Materialien wie Paraffin gefüllt werden, um besondere Eigenschaften zu erhalten. Neben Bierschaum ist auch der Badeschaum eine Möglichkeit Schäume mit ihrem außergewöhnlichem Verhalten kennenzulernen. Das geschäumte Materialgemisch erhält dabei aber typischerweise nicht durchschnittliche Materialeigenschaften, sondern es können Eigenschaften der einzelnen Materialien teilweise kombiniert werden; z.B. erhält ein Metall-Paraffinschaum eine recht hohe Wärmeleitfähigkeit vom Metall gepaart mit einer hohen Wärmekapazität und vor Allem mit einem günstigen Schmelzpunkt (45-80°C) vom Paraffin und ist damit ein sehr effizienter Latentwärmespeicher. In der Natur finden sich Schaumstrukturen zum Beispiel in Knochen, die bei hoher Stabilität ein deutlich geringeres Gewicht als ein massives Material haben. Aber auch für Knochenimplantate sind Metallschäume aus Titan durch die hohe Stabilität bei geringem Gewicht und guter Verträglichkeit sehr interessant. Problematisch ist für den Einsatz von Metallschäumen, dass noch viele quantitative Messgrößen fehlen, die Herstellung noch recht teuer ist, und insbesondere nur in kleinen Größen produziert werden kann. Als Unterscheidungsmerkmal hat sich neben der Unterscheidung in offen oder geschlossen porigen Schaum die ppi-Zahl als Maß für die Porendichte etabliert, dabei zählt man die Poren pro Inch (Zoll, entspricht 2,54 cm). Dazu erfasst man auch die mittlere Porengröße (Durchmesser), ihre Standardabweichung, die Porosität, die mittlere Stegdicke und deren Form. Weiterhin können sich Größen in verschiedenen Richtungen im Material unterscheiden, und dadurch merklich deren Eigenschaften verändern. Für die Herstellung von Metallschäumen gibt es unterschiedliche Verfahren: Zwei typische Vertreter sind das Pressen mit dem anschließenden Schmelzen von gemischtem Metall- und Metallhybridpulvern für geschlossen porige feste Schäume oder Gießverfahren, wo der Metallschaum für offen porige Materialien durch keramische Negativabbildungen von Polyurethan-Schäumen nachempfunden wird. Schon früh waren Schäume als möglichst dichte Packungen ein Forschungsfeld in der Mathematik. Im Jahr 1994 haben Weaire-Phelan eine noch optimalere regelmäßige Schaumstruktur veröffentlicht, die in der Architektur des zu den olympischen Sommerspielen 2008 in Peking errichteten Nationalen Schwimmzentrums verewigt wurde. Das ebenfalls zu den Sommerspielen errichtete Vogelnest hat im Gegenteil eine zufälligere Struktur. Lange hatte man keine verlässlichen Aussagen über die Wärmeleitfähigkeit von Metallschäumen. Bei einer Leitfähigkeit von etwa 200 W/(mK) von Aluminium erreicht ein Metallschaum Leitfähigkeiten zwischen 5-13 W/(mK) während man bei Luft von einer Leitfähigkeit von etwa 0.025 W/(mK) ausgehen kann. Außerdem haben Metallschäume einen hohen Oberflächenanteil, dies bezeichnet die vorhandene Oberfläche im Verhältnis zum Volumen. Während ein voller Metallwürfel ein Verhältnis von etwa Eine interessante Fragestellung ist auch, ab welcher Porengröße die natürliche Konvektion in mit Luft gefüllten Metallschäumen eine Rolle gegenüber der Wärmeleitung spielt. Die relevante Größe ist hier die Rayleigh-Zahl, die für Metallschäume typischer Porengrößen ergibt, dass die natürliche Konvektion zu vernachlässigen ist. Für die Simulation wird der komplette Raum des Metallschaums diskretisiert, und es gibt eine Funktion, die als Indikatorfunktion anzeigt, ob an diesem Punkt Metall oder Luft vorliegt. Hier können sowohl aus an der Hochschule Pforzheim durchgeführten Schnitten rekonstruierte Schaumstrukturen abgebildet werden, aber auch künstlich mit Algorithmen erzeugte Schäume für die Simulation abgebildet werden. Bei der künstlichen Erzeugung von Schäumen ist die Voronoi-Zerlegung ein wichtiger Algorithmus zur Bestimmung der Poren. Den eigentlichen Wärmetransport im Metallschaum wird durch die Wärmeleitungsgleichung Die Phasenfeldmethode und die Software Pace3D stammt ursprünglich aus der Simulation von Erstarrungs- und Schmelzvorgängen auf der Mikrometerskala. Metalle erstarren in Form von sogenannten Dendriten. Das sind Kristalle, die eine gewisse Ähnlichkeit mit Schneeflocken aufweisen. Eine interessante Anwendung von Metallschäumen bietet das mutige Silent Power PC Projekt, in dem ein Metallschaum den einen Rechner effizient kühlen soll. Aus den bisherigen Erkenntnissen der Arbeitsgruppe ist anzunehmen, dass ein Großteil der Kühlleistung in einem solchen System auf der Wärmeleitung liegt - für einen Einfluss der natürlichen Konvektion scheint die Porengröße zu klein zu sein. Die Faszination für Wissenschaft inspiriert Anastasia August nicht nur in der Forschung, sondern sie demonstriert sie auch auf Science Slams und im FameLab. Sie hielt dort Vorträge über ihr Forschungsgebiet und auch über das sehr unterschätzte Thema der Stetigkeit und die Anwendung auf Temperaturen auf der Erdkugel. Mit dem Vortrag auf dem Science Slam Vorentscheid in Esslingen zu Metallschäumen hat sie sich für die Meisterschaft am 6. Dezember qualifiziert. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 20 Nov 2014 | Graphpartitionierung | 00:35:51 | |||||||||||||||||
Ein Graph ist eine Menge von Knoten und Kanten zwischen diesen Knoten. Man unterscheidet zwischen gerichteten Graphen, wo Einbahnstraßen darstellbar sind, oder den ungerichteten Graphen, wo Beziehungen zwischen zwei Knoten immer beidseitig sind. Beispiele sind die graphische Darstellung von Beziehungen in einem sozialen Netz oder Straßennetze, für deren Verarbeitung das Forschungsgebiet von Christian Schulz immer bedeutender wird, wie wir in seinem Gespräch mit Gudrun Thäter erfahren. Eine wichtige Aufgabe im Umgang mit Graphen ist die Aufteilung (oder fachsprachlich Partitionierung), von Graphen in kleinere Teile. Dies kommt z.B. der Parallelisierung der Arbeit auf den Graphen zugute, und ist unumgänglich, wenn Graphen eine Größe haben, die nicht mehr von einem Prozessor bearbeitet werden kann. Ein wichtiges Merkmal ist hier, die Aufteilung möglichst gleichmäßig vorzunehmen, damit die Aufteilung von z.B. Rechenzeit gleichmäßig erfolgt, und gleichzeitig wenig Kommunikation zwischen der Bearbeitung der Einzelteile erforderlich ist. Es geht um eine möglichst gute Skalierbarkeit der Graphverarbeitung. Ein wichtiges Anwendungsproblem ist die Routenplanung, bei der zwischen zwei Punkten auf der Erde die zeitlich kürzeste Verbindung berechnet werden soll. In der Informatik ist der Dijkstra-Algorithmus der passende Basis-Algorithmus für diese Aufgabe, doch er ist für große Graphen in seiner ursprünglichen Form sehr ineffizient. In Kombination mit einer passenden Graphpartitionierung und Algorithmen kann man das Verfahren deutlich effizienter ausführen und beschleunigen. Ein klassisches Verfahren zur Aufteilung ist das Mehrschichtverfahren über die Laplace-Matrix, wo ausgenutzt wird, dass zwischen den Eigenwerten der Matrix und der Schnittstruktur des Graphen enge Zusammenhänge bestehen. Dieses Verfahren wurde zum Mehrschichtverfahren für Graphen weiterentwickelt, bei dem in einer sogenannten Kontraktion benachbarte Knoten und parallele Kanten jeweils zusammengeführt werden, und der Graph zu einem kleinen und kantengewichteten Graph vereinfacht wird. Schließlich wird das Problem auf einem vereinfachten, groben Gitter gelöst, und dann jeweils mit lokalen Suchen auf feinere Graphen erweitert. Für die Kontraktion werden Heuristiken und Kantenbewertungsfunktionen verwendet. Ein weiterer Ansatz sind auch evolutionäre Algorithmen. Dabei wurde eine allgemeinere Umgebung geschaffen, die auf eine weite Klasse von Optimierungsproblemen angewendet werden kann. Die Graphentheorie ist natürlich auch Teil der diskreten Mathematik, und besonders berühmt ist auch das Traveling Salesperson Problem. Gleichzeitig ist das Thema aber auch in der Theoretischen Informatik, im Algorithm Engineering und in der Software-Entwicklung beheimatet. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 27 Nov 2014 | Systembiologie | 01:33:01 | |||||||||||||||||
Auf den Vorschlag von Henning Krause verbreiteten viele Forschende unter dem Hashtag #1TweetForschung ihr Forschungsthema in Kurzform. So auch Lorenz Adlung, der in der Abteilung Systembiologie der Signaltransduktion am Deutschen Krebsforschungszentrum in Heidelberg die mathematische Modellbildung für biologische Prozesse erforscht. Bei der Anwendung einer Chemotherapie leiden Krebspatienten oft unter Blutarmut. Hier kann neben der Bluttransfusion das Hormon Erythropoetin, kurz EPO, helfen, da es die körpereigene Erzeugung von roten Blutkörperchen (Erythrozyten) unterstützt. Leider ist EPO als Dopingmittel bekannt, und um dem Doping noch deutlicher Einhalt zu gebieten, wurde im November 2014 in Deutschland ein Entwurf eines Anti-Doping-Gesetz vorgelegt. Trotz gängigem Einsatz und erprobter Wirkung von EPO ist die genaue Wirkung von EPO auf Krebszellen nicht bekannt. Daher verfolgt Lorenz Adlung den Ansatz der Systembiologie, um im Zusammenwirken von Modellbildung und Mathematik, Biologie und Simulationen sowohl qualitativ und quantitativ analysieren und bewerten zu können. Vereinfacht sind rote Blutkörperchen kleine Sauerstoff-transportierende Säckchen aus Hämoglobin, die auch die rote Farbe des Bluts verursachen. Sie stammen ursprünglich aus Stammzellen, aus denen sich im Differenzierungs-Prozess Vorläuferzellen bzw. Progenitorzellen bilden, die wiederum durch weitere Spezialisierung zu roten Blutkörperchen werden. Da es nur wenige Stammzellen gibt, aus denen eine unglaubliche große Anzahl von Trillionen von Blutkörperchen werden müssen, gibt es verschiedene Teilungs- bzw. Proliferationsprozesse. Das Ganze ergibt einen sehr komplexen Prozess, dessen Verständnis zu neuen Methoden zur Vermehrung von roten Blutkörperchen führen können. Den durch Differenzierung und Proliferation gekennzeichnete Prozess kann man mathematisch beschreiben. Eine zentrale Ansichtsweise in der Systembiologie der Signaltransduktion ist, Zellen als informationsverarbeitende Objekte zu verstehen, die zum Beispiel auf die Information einer höheren EPO-Konzentration in der Umgebung reagieren. Von diesem Ansatz werden durch Messungen Modelle und Parameter bestimmt, die das Verhalten angemessen beschreiben können. Diese Modelle werden in Einklang mit bekannten Prozessen auf molekularer Ebene gebracht, um mehr über die Abläufe zu lernen. Die erforderlichen quantitativen Messungen basieren sowohl auf manuellem Abzählen unter dem Mikroskop, als auch der Durchflusszytometrie, bei der durch Streuung von Laserlicht an Zellen durch Verwendung von Markern sogar Aussagen über die Zelloberflächen getroffen werden können. Zusätzlich kann mit der Massenspektrometrie auch das Innere von Zellen ausgemessen werden. In diesem Anwendungsfall werden die mathematischen Modelle in der Regel durch gekoppelte gewöhnliche Differenzialgleichungen beschrieben, die Zell- oder Proteinkonzentrationen über die Zeit beschreiben. Die Differenzialgleichungen und deren Parameter werden dabei sowohl mit Messungen kalibriert, als auch mit den Kenntnissen in der Molekularbiologie in Einklang gebracht. Die Anzahl der Parameter ist aber oft zu hoch, um naiv auf geeignete zu den Messungen passende Werte zu gelangen. Daher wird unter anderem das Latin Hypercube Sampling verwendet, um schnell nahe sinnvollen Parameterwerten zu gelangen, die durch gradienten-basierte Optimierungsverfahren verbessert werden können. Die Basis für diese Art von Optimierungsverfahren ist das Newton-Verfahren, mit dem man Nullstellen von Funktionen finden kann. Ein wichtiger Aspekt im Umgang mit Messergebnissen ist die Berücksichtigung von Messfehlern, die auch vom Wert der Messung abhängig verstanden werden muss- denn nahe der Messgenauigkeit oder der Sättigung können die relativen Fehler extrem groß werden. Die Bestimmung der Modellparameter ist schließlich auch ein Parameteridentifikationsproblem, wo insbesondere durch eine Sensitivitätsanalyse auch der Einfluss der geschätzten Parameter bestimmt werden kann. Sowohl die Parameter als auch die Sensitivitäten werden mit den biologischen Prozessen analysiert, ob die Ergebnisse stimmig sind, oder vielleicht auf neue Zusammenhänge gedeuten werden können. Hier ist die Hauptkomponentenanalyse ein wichtiges Werkzeug, um zentrale beeinflussende Faktoren erfassen zu können. Ein wichtiges Ziel der Modellbildung ist die numerische Simulation von Vorgängen, die als digitale Experimente sich zu einem eigenen Bereich der experimentellen Forschung entwickelt haben. Darüber hinaus ermöglicht das digitale Modell auch die optimale Planung von Experimenten, um bestimmte Fragestellungen möglichst gut untersuchen zu können. Die Umsetzung auf dem Computer erfolgt unter anderem mit Matlab, R (The R Project for Statistical Computing) und mit der spezialisierten und freien Software D2D - Data to Dynamics. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 11 Dec 2014 | Topologie | 01:16:08 | |||||||||||||||||
Prof. Dr. Wolfgang Lück befasst sich am HIM (Hausdorff Research Institute for Mathematics) und dem Mathematisches Institut der Universität Bonn mit der Topologie von Mannigfaltigkeiten und Flächen wie auf einem Torus oder einer Kugel. Speziell für Kugeln und Kreise gibt es die Sphären-Notation Auch wenn Flächen lokal ähnliche Eigenschaften haben, kann die Situation global ganz anders aussehen: So unterscheidet sich die Vorstellung einer flachen Erde lokal nicht von der Kugelform der Erde, global sieht es aber ganz anders aus. Ebenso kennen wir auch jetzt noch nicht sicher die Topologie des Weltalls. Dazu beschränkt sich unser Vorstellungsraum oft auf drei Dimensionen, obwohl schon die relativistische Physik uns lehrt, unsere Umgebung als Raumzeit in 4 Dimensionen zu verstehen. Bei der Klassifikationen von Flächen auf unterschiedlichen Körpern verwendet man Homöomorphismen um ähnliche Flächen einander zuzuordnen, und letztlich unterscheiden sich die Flächenklassen dann nur noch durch die Anzahl der Löcher bzw. dem Geschlecht, was dann auch die Eigenschaften der Flächen bestimmt. Ein Weg das Geschlecht der Fläche zu bestimmen ist die Triangularisierung, eine andere Möglichkeit bietet die Analyse des Spektrums eines Operators wie dem Laplace-Operators, das auch in der Topologie von Graphen zum Einsatz kommen kann. Ein Beispiel für die Anwendung des Laplace-Operators ist die Wärmeleitungsgleichung, die zwar die lokalen Eigenschaften des Wärmetransports beschreibt, jedoch das Wärmegleichgewicht nach unendlicher Zeit die globalen Zusammenhänge beinhaltet. Ein wichtiger Begriff ist hier der Integralkern, der hilft Lösungen durch Integraloperatoren darzustellen. Ein wichtiger mathematischer Begriff ist dabei der Besonderes Interesse liegt in der Topologie auf Invarianten, wie der Fundamentalgruppe, mit der man auch den Fundamentalsatz der Algebra beweisen kann. Ein weiteres Beispiel für eine Invariante ist die Windungszahl, die gerade in der Funktionentheorie zum Residuensatz und effizienten Integralberechnungsmethoden führt. Dabei entstehen oft nicht kommutative Verknüpfungen, wie man es zum Beispiel von der Matrizenmultiplikation oder den Symmetriegruppen kennen kann. Ein elementarer Einstieg in die Topologie ist auch über die Knotentheorie möglich, wo ebenso Knoten-Invarianten gefunden werden können, und über zum Beispiel Jones-Polynome klassifiziert werden können. Im weiteren Gespräch geht es um Themen wie die unterschiedlichen Bilder der Mathematik in Gesellschaft, Schule und Universität, die Bedeutung der Mathematik für Gesellschaft, die Ausbildung für Industrie und das Lehramt, und über den Stand und Möglichkeiten der Gleichberechtigung und Förderung von Frauen in der Wissenschaft. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 18 Dec 2014 | Risikobewertung | 00:26:41 | |||||||||||||||||
Prof. Dr. Wolfgang Härdle war im Rahmen des Workshop zu High Dimensional, High Frequency and Spatial Data in Karlsruhe und sprach mit Gudrun Thäter über sein Forschungsgebiet. Er befasst sich an der Humboldt-Universität zu Berlin mit der Bewertung von Risiken und ist am Lehrstuhl der Nachfolger von Ladislaw Bodjevich, der unter anderem für seine Arbeiten zum Gesetz der kleinen Zahlen berühmt geworden ist: Es sagt aus, dass auch wenn alle 37 Roulette-Zahlen gleich wahrscheinlich sind, nach 37 Würfen im Durchschnitt nur etwa 2/3 der Zahlen aufgetreten sind. Damit steht es nur scheinbar in gewissem Kontrast zum Gesetz der großen Zahlen, das bestimmt, wie die Auftrittshäufigkeit sich für viele Würfe der Gleichverteilung annähert. Das Flanken-Maß ist eine Eigenschaft von Profit and Loss (PnL, GuV)-Funktionen oder Zufallsvariablen, die die Dicke von Flanken oder Entferntheit von seltenen Ereignissen modelliert. Schon Ladislaw Bodjevich hat erkannt, dass das die Bewertung von Extremrisiken und wenige vorhandene Daten einen Widerspruch darstellt. Die Normalverteilung ist die Grenzverteilung gewichteter Zufallsgrößen, wenn der Grenzwert existiert, also bei vielen Ereignissen das Gesetz der großen Zahlen zum Einsatz kommen kann. Bei wenigen Ereignissen gelangt man zur Poisson-Verteilung. Obwohl sie theoretisch viele Prozesse gut beschreiben sollte, funktioniert die Normalverteilung in der Realität aus vielen Gründen oft schlechter als erwartet: Sich verändernde Prozesse können Mischverhältnisse von an sich normal-verteilten Bestandteilen verändern, ebenso kann sich die Volatilität bzw. die Streuung um den Erwartungswert über die Zeit verändern. Es kann aber auch eine vollkommene andere Verteilung vorliegen wie zum Beispiel die Extremwertverteilung, Weibull-Verteilung mit algebraisch abfallenden Tails oder der Pareto-Verteilung. Leider ist die stochastische Konvergenz von Extermwertverteilungen sehr schlecht, und erschwert so Vorhersagen und Bewertungen. So wurden strukturierte Finanzprodukte mit multivariaten Modellen und einer Normalverteilungsannahme viel zu vereinfacht modelliert. So waren CDO-Produkte daher vor der Finanzkrise ab 2007 viel zu billig und hatten einen beträchtlichen Anteil an der Krise. Die Risikobewertung ist aber nicht nur für die Bewertung von Katastrophen-Bonds für Versicherungen gegen Erdbeben wichtig, sondern auch für die Analyse von EEG von Kindern. Sie hilft aber auch den Risikofaktor Mensch im Sinne der Behaviour Finance zu verstehen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 25 Dec 2014 | Teichmüllerkurven | 00:48:06 | |||||||||||||||||
Jonathan Zachhuber war zum 12. Weihnachtsworkshop zur Geometrie und Zahlentheorie zurück an seine Alma Mater nach Karlsruhe gekommen und sprach mit Gudrun Thäter über Teichmüllerkurven. Kurven sind zunächst sehr elementare ein-dimensionale mathematische Gebilde, die über den komplexen Zahlen gleich viel reichhaltiger erscheinen, da sie im Sinne der Funktionentheorie als Riemannsche Fläche verstanden werden können und manchmal faszinierende topologische Eigenschaften besitzen. Ein wichtiges Konzept ist dabei das Verkleben von Flächen. Aus einem Rechteck kann man durch Verkleben der gegenüberliegenden Seiten zu einem Torus gelangen (Animation von Kieff zum Verkleben, veröffentlicht als Public Domain): Polynome in mehreren Variablen bieten eine interessante Art Kurven als Nullstellenmengen zu beschreiben: Die Nullstellen-Menge des Polynoms Auch wenn die entstehenden abstrakten Beschreibungen nicht immer anschaulich sind, so erleichtern die komplexen Zahlen den Umgang mit Polynomen in einem ganz wichtigen Punkt: Der Fundamentalsatz der Algebra besagt, dass der Grad des Polynoms gleich der Anzahl der Nullstellen in ihrer Vielfachheit ist. Also hat nun jedes nichtkonstante Polynom mindestens eine Nullstelle, und über den Grad des Polynoms wissen wir, wie viele Punkte sich in der Nullstellenmenge bewegen können, wenn wir an den Koeffizienten Veränderungen vornehmen. Eine gute Methode die entstehenden Flächen zu charakterisieren ist die Bestimmung möglicher geschlossener Kurven, und so gibt es beim Torus beispielsweise zwei unterschiedliche geschlossene Kurven. Die so enstehende Fundamentalgruppe bleibt unter einfachen Deformationen der Flächen erhalten, und ist daher eine Invariante, die hilft die Fläche topologisch zu beschreiben. Eine weitere wichtige topologische Invariante ist das Geschlecht der Fläche. Die Teichmüllerkurven entstehen nun z.B. durch das Verändern von einem Koeffizienten in den Polynomen, die uns durch Nullstellenmengen Kurven beschreiben- sie sind sozusagen Kurven von Kurven. Die entstehenden Strukturen kann man als Modulraum beschreiben, und so diesen Konstruktionen einen Parameterraum mit geometrischer Struktur zuordnen. Speziell entstehen Punkte auf Teichmüllerkurven gerade beim Verkleben von gegenüberliegenden parallelen Kanten eines Polygons; durch Scherung erhält man eine Familie von Kurven, die in seltenen Fällen selbst eine Kurve ist. Ein Beispiel ist das Rechteck, das durch Verkleben zu einem Torus wird, aber durch Scherung um ganz spezielle Faktoren zu einem ganz anderen Ergebnis führen kann. Die durch Verklebung entstandenen Flächen kann man als Translationsflächen in den Griff bekommen. Hier liefert die Translationssymmetrie die Methode um äquivalente Punkte zu identifizieren. Für die weitere Analyse werden dann auch Differentialformen eingesetzt. Translationen sind aber nur ein Beispiel für mögliche Symmetrien, denn auch Rotationen können Symmetrien erzeugen. Da die Multiplikation in den komplexen Zahlen auch als Drehstreckung verstanden werden kann, sind hier Rotationen als komplexe Isomorphismen ganz natürlich, und das findet man auch in den Einheitswurzeln wieder. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 08 Jan 2015 | Fußgänger | 00:25:44 | |||||||||||||||||
Auch Menschenströme können mathematisch beschrieben und mit geeigneten Modellen auch simuliert werden. Damit können große Veranstaltungen im Vorfeld besser geplant und ausgelegt werden, damit Engpässe oder sogar Katastrophen wie bei der Love-Parade 2010 möglichst verhindert werden. Henrieke Benner hat dazu die Parameter für die Simulation von Fußgängern im Gegenstrom kalibriert und spricht mit Gudrun Thäter über die Verfahren, Herausforderungen und Erkenntnisse. Mathematisch betrachtet sie die Fußgänger in einem mikroskopischen Modell, wo jede Person als eigenes Objekt simuliert wird. Entsprechend der Situation wirken nun virtuelle Kräfte auf diese Objekte, so verhindert eine virtuelle Abstoßungskraft zwischen zwei Personen, dass diese zusammenstoßen. Die betrachtete Simulation wird durch eine Vielzahl von Parametern konfiguriert, die mit realen Experimenten kalibriert werden müssen. Dies kann durch eine Optimierung der Parameter gelöst werden, die die Simulation den Experimenten möglichst weitgehend annähert. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 15 Jan 2015 | Geometrische Analysis | 00:41:35 | |||||||||||||||||
Geometrie und Analysis sind auf den ersten Blick zwei sehr unterschiedliche Disziplinen in der Mathematik. Wie sie jedoch wunderbar zusammenpassen, erläutert Prof. Dr. Tobias Lamm im Gespräch mit Gudrun Thäter. Ein klassisches Beispiel für die geometrische Analysis ist das Problem der Dido: Wie kann man bei festgelegtem Umfang ein möglichst großes Gebiet abstecken? Es geht also darum den Flächeninhalt unter einer Nebenbedingung zu maximieren, und das ist ein typisches Variationsproblem, das stark von der gegebenen Geometrie abhängt. Ein anderes Beispiel sind Minimalflächen, wie man sie beim Olympiastadion in München und Seifenblasen sehen kann. Überraschenderweise sind Minimalflächen nicht immer eindeutig. Ein Weg dies zu analysieren geht über die Beschreibung des Problems durch Partielle Differentialgleichungen. Oft kann man über das Maximumsprinzip die Eindeutigkeit beweisen: Bei linearen elliptischen partiellen Differentialgleichungen sagt das Prinzip aus, dass das Maximum entweder auf dem Rand angenommen wird oder konstant ist. Betrachtet man nun die Differenz zweier angenommen unterschiedlicher Lösungen zu gleichen Randwerten, so folgt, dass die Differenz wegen der Linearität auch eine Lösung ist, und wegen des Maximumprinzips konstant 0 ist. Damit waren als Resultat dieses Widerspruchbeweises die zwei Lösungen identisch. Bei allgemeineren, u.a. nicht-linearen, Problemstellungen muss dieses Prinzip nicht unbedingt gelten, und so kann es zu mehreren Lösungen zur gleichen Aufgabenstellung kommen. Aktuelle Forschungsbereiche in der geometrischen Analysis sind der mittlere Krümmungsfluss und die geometrische Evolutionsgleichung im Allgemeinen. Ebenso geht es um die Frage, mit welcher minimalen Regularität für die Anfangsdaten, noch eine Lösung rekonstruiert werden kann. Ein weiteres Forschungsgebiet sind die recht jungen Willmore-Flächen. Das Willmore-Funktional ist sehr eng verwandt zur Plattengleichung, d.h. der Approximation des Durchbiegens von Platten. Es hat aber auch Anwendungen in der Zellbiologie in der Modellierung der Form der Zellen. Letztlich kommt es auch in der allgemeinen Relativitätstheorie zum Einsatz. Sehr aktuell ist der Beweis der Poincaré-Vermutung, die 2002 von Perelman bewiesen werden konnte. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 22 Jan 2015 | Kaufverhalten | 00:29:12 | |||||||||||||||||
Bei der stochastischen Analyse von Kaufverhalten konzentriert man sich besonders auf die Aspekte des Kaufzeitpunkts, der Produktwahl und der Kaufmenge, um im Wettbewerb einen Vorteil gegenüber der Konkurrenz zu erhalten. Kristina Cindric führt im Gespräch mit Gudrun Thäter aus, wie sie auf Basis großer Datenmengen von anonymisierten Vertragsabschlüssen über ein Jahr Analysen erstellt, Modelle entworfen, trainiert und die entstehenden Prognosen getestet hat. Die auftretenden stochastischen Modelle können sehr vielseitig sein: So kann der Kaufzeitpunkt beispielsweise durch einen stochastischen Prozess mit exponentieller Verteilung modelliert werden, für die Produktwahl kann ein Markow-Prozess die wahrscheinlichsten nächsten Käufe abbilden. Ein zentrales Konzept für die Analyse und das Training von Modellen ist dann die Parameterschätzung, die die tatsächliche Ausgestaltung der Modelle aus den Daten bestimmt. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 29 Jan 2015 | Extremereignisse | 00:26:28 | |||||||||||||||||
Sebastian Lerch befasst sich mit der Vorhersage von Extremereignissen, zum Beispiel bei Stürmen und extrem starken Regenfällen und deren Auswirkung auf Fluten oder auch bei Ausnahmeereignissen in der Finanzindustrie. Das Dilemma ist dabei, dass die öffentliche Bewertung oft nur nach eventuell nicht vorhergesagten Katastrophen erfolgt, wie bei dem Erdbeben von L’Aquila, das sogar zur in erster Instanz Verurteilung von Wissenschaftlern führte. Tatsächlich gibt es Fälle erfolgreicher Erdbebenvorhersage, doch leider sind dies nur seltene Ereignisse. Die grundsätzliche Schwierigkeit liegt darin, ein angemessenes Modell für die Risikobewertung zu finden, auch wenn manche Ereignisse nur selten oder in bestimmter Umgebung sogar noch nie aufgetreten sind, und so kaum Daten vorliegen. Die Lösung liegt darin auf probabilistische Vorhersagen zu setzen. Hier wird kein deterministischer fester Wert vorhergesagt, sondern die stochastische Verteilung, in der man die Wahrscheinlichkeit für alle Ereignisse definiert. Verschiedene probabilistische Vorhersagen können mit Hilfe des Continuous Rank Probability Score (CRPS) zu Beobachtungen verglichen und evaluiert werden. Die CRPS ist dabei ein Vertreter der Proper Scoring Rules, da die wahre Verteilung diesen Score tatsächlich maximiert. Eine Herausforderung verbleibt die Frage nach einer geeigneten Vermittlung von probabilistischen Aussagen, wie sie uns in der Regenwahrscheinlichkeit täglich in der Wettervorhersage begegnet, und leider selten richtig verstanden wird. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 05 Feb 2015 | Papierrechner | 01:18:00 | |||||||||||||||||
Joachim Breitner veranstaltete im FabLab Karlsruhe einen Workshop auf dem er unter anderem seinen Taschenrechner auf Papier vorstellte. Den Rechner hat er mit einem speziellen Digitalstift realisiert, dessen genaue Funktionsweise analysiert wurde. Im Workshop ging es speziell um den Tiptoi-Stift, der auf dem Papier ein fast unsichtbares Punktemuster analysiert. Dieses Punktemuster macht das Papier zu digitalem Papier. Hier werden immer im Code 16 Punkte zu einem Block zusammengefasst, von denen die Punkte am linken und oberen Rand zur Erkennung, und die restlichen neun Punkte die eigentliche Information als Zahl mit Prüfbits beinhalten. Dabei entsprechen vier Punkte etwa einem Millimeter und daher sind die Muster, die sich auf den aktiven Bereichen wiederholen, mit dem Auge kaum zu erkennen. Die Funktionen des Stifts werden als GME-Dateien wie auf einen USB-Stick kopiert, und diese konnten in einem längeren Prozess zum Großteil analysiert werden. Zunächst wurden die im freien Ogg Vorbis-Format kodierten Tondateien gefunden, die über eine einfache Substitutions-Chiffre verschleiert wurden. Im Folge der weiteren Analyse wurden die Programme zu den Papiermustern gefunden, und aus diesen konnte die Maschinensprache der Stifte im Großteil bestimmt werden. Das System reagiert auf gescannte Codes, und kann dann verschiedene Aktionen wie das Abspielen von Audio, Variablen setzen, Rechnungen durchführen und Variablen abfragen. Ein Rätsel verblieb, warum die berechneten Werte aus den Papiercodes nicht mit den Kennungen in den Programmen übereinstimmten. Dies konnte man durch Wechsel des Stifts in einen Debug-Modus durch Drücken der Minus-Taste beim Anschalten und anschließend der Plus-Taste nachvollziehen, denn dann liest der Stift die in der Maschinensprache verwendeten Codes auf Chinesisch vor. Zum Verständnis braucht man da nur eine Tabelle der chinesischen Zahlen von 1 bis 10. Aber auch diese Zuordnung konnte inzwischen analysiert und gelöst werden. Damit können nun komplett eigene Seiten mit Papier-Code und zugehörigen GME-Programmen von jedem selbst erstellt werden, dazu wurde das tttool entwickelt, mit dem sowohl die Programme in einer speziellen Sprache, wie auch die zugehörigen Punktemuster erzeugt werden können. Das Erstellen druckbarer Seiten erfordert dann nur noch ein geeignetes Grafikprogramm und passende Hintergrundbilder, wie Joachim Breitner im Gespräch mit Sebastian Ritterbusch darlegt. Literatur und Zusatzinformationen | |||||||||||||||||||
| 19 Feb 2015 | Strömungslärm | 01:24:12 | |||||||||||||||||
Die Gründer Carlos Falquez, Iris Pantle und Balazs Pritz aus dem Karlsruher Institut für Technologie (KIT), befassen sich mit Verfahren für Strömungslärmprognose und bieten diese Ingenieurbüros und Unternehmen zur Nutzung auf ihrer Cloud-Simulationsplattform NUBERISIM an. Während für viele Strömungen die inkompressiblen Navier-Stokes-Gleichungen ausreichen, kommen hier kompressible Gleichungen zum Einsatz. Dies ändert das Gleichungssystem von einem dominant elliptischen zu einem dominant hyperbolischen System, dem die numerischen Verfahren Rechnung tragen müssen. Der Definition des Simulationsgebiets und den an dessen Rändern festzulegenden Randbedingungen kommt hier eine besondere Bedeutung zu: Beides muss aufeinander abgestimmt sein, jede ins Simulationsgebiet einlaufende Störung besitzt selbst wieder die Größenordnung akustischer Wellen und kann daher vom eigentlichen Simulationsergebnis, dem durch die Strömung erzeugten Schall, schlecht getrennt werden. Daneben ergeben sich weitere Herausforderungen, wie den Einsatz von Verfahren höherer Ordnung, um die Wellendispersion zu bewahren, deren Erhaltung in einer typischen Strömungssimulation normalerweise weder forciert wird noch das Ergebnis signifikant verbessern würde. Schließlich sind solche Verfahren hoch-instationär, so dass sich für realistische Fragestellungen äußerst lange Rechenzeiten ergeben. Dadurch wurden sie in der Vergangenheit nur in der akademischen Forschung untersucht und angewendet. Der Schritt zur kommerziellen Nutzung schien lange undenkbar. Durch moderne Parallelisierungstechniken und Cloud-Systeme jedoch steht plötzlich auch kleineren Unternehmen wie z.B. Ingenieursdienstleitern ausreichend Rechenkapazität zur Verfügung – theoretisch, denn der Zugang hierzu ist immer noch Eingeweihten vorbehalten. Darum haben die Gründer die Idee entwickelt, solche Verfahren nicht nur als Software, sondern als Plattform einschließlich Nutzeroberfläche anzubieten, gerade so wie bei einer konventionellen Software – nur eben über einen Browser anzusteuern. Die Plattform wird voraussichtlich im März zugänglich gemacht. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 26 Feb 2015 | Wasserraketen | 00:30:09 | |||||||||||||||||
Gabriel Thäter ist im Rahmen eines BOGY-Praktikums zum Institut gekommen, um einen Eindruck von der Forschungstätigkeit in der angewandten Mathematik zu erhalten. Dazu befasste er sich mit der Simulation, Auslegung und Optimierung von Wasserraketen, die durch Impulserhaltung ihre Beschleunigung erhalten. Sein Interesse an der Raketentechnik entstand durch die Kerbal Space Program Simulation, in der Raketen und Flugzeuge zur Erfüllung verschiedener Aufträge aufgebaut werden. Die Wasserraketen unterscheiden sich unter anderem durch ihre Bauform, dem zur Befüllung zur Verfügung stehenden Volumen, wie viel Wasser darin mit welchem Druck eingefüllt wird und welche Düse verbaut wurde. Der erste Ansatz die Auswirkung der Düse durch den Druckunterschied mit einer laminaren Strömung zu berechnen, führte zu unrealistischen Ergebnissen, was auf Basis der hohen Reynolds-Zahl zu erwarten war. Ein Ansatz über ein turbulentes Strömungsmodell führte zu sinnvollen Werten für die Rückstoßgeschwindigkeit in diskretisierter zeitlicher Abhängigkeit. Die Berechnung der Steighöhe ist besonders durch die Schwerkraft und den Luftwiderstand abhängig. Neben der Berücksichtigung des sich stark verändernden Gewichts, ist die Bestimmung des geeigneten cW-Werts für den Strömungswiderstand eine große Herausforderung. Neben dem Vergleich mit einfachen Körpern wie Zylindern und Kugeln konnte eine Parameteridentifikation aus experimentellen Messwerten den cW-Wert sinnvoll bestimmen. Die praktische Ausführung des Experiments verfolgt man am Besten bei unseren Kollegen bei Methodisch Inkorrekt, die beim 31C3 ihre Wasserrakete live im Sendezentrum zündeten. Natürlich gibt es auch reine Luftraketen, die beeindruckende Höhen erreichen können. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 12 Mar 2015 | Klothoiden | 00:32:04 | |||||||||||||||||
Klothoiden sind Kurven, die 1794 von Jakob I. Bernoulli zuerst beschrieben wurden. Er hatte die Form eines Metallstreifens untersucht, der von einem Gewicht an einem Ende verbogen wird, während das andere Ende eingespannt ist. Als Resultat des elastischen Verhaltens ist dann die Krümmung proportional zur Kurvenlänge. Viele weitere Eigenschaften von Kurven mit dIeser Eigenschaft wurden dann von Leonhard Euler über den Rahmen des Gedankenexperiments von Bernoulli hinaus bewiesen , wie zum Beispiel die Position der asymptotischen Endpunkte. Im Straßen- und Schienenbau sind Klothoiden ausgezeichnete Übergangsbögen zwischen geraden Strecken und Kurven, da diese Kurve die Krümmung zwischen den beiden Abschnitten gleichmäßig anpasst. Bei der Planung von Schienentrassen wurde diese Eigenschaft vor etwa 100 Jahren schon ausgenutzt. Eine aktuelle wichtige Anwendung ist die Abbildung der Straßen in Fahrassistenzsystemen, wo passend parametrisierte Klothoiden große Vorteile gegenüber Splines besitzen, wie Gotami Heller im Gespräch mit Gudrun Thäter erklärt. Um Klothoiden tatsächlich im Computermodell benutzen zu können, muss eine möglichst adäquate Approximation gesucht und implementiert werden, die die nötige Glattheit in der Kurve erhält. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 19 Mar 2015 | Flipped Classroom | 03:05:01 | |||||||||||||||||
An Pädagogischen Hochschulen werden Lehrerinnen und Lehrer für fast alle Schulformen ausgebildet, es gibt sie inzwischen in Deutschland nur noch in Baden-Württemberg. Beispielsweise seien die Pädagogische Hochschule Heidelberg und die Pädagogische Hochschule Karlsruhe genannt- hier in Karlsruhe gibt es zusätzlich auch eine Abteilung für Didaktik an der Fakultät für Mathematik am KIT. An den pädagogischen Hochschulen werden aber nicht nur Pädagogik und Didaktik unterrichtet, sondern auch die entsprechenden Fachrichtungen und jeweilige didaktische Konzepte in diesen Fachrichtungen. Christian Spannagel unterrichtet so als Professor für Mathematik und Informatik in den Fächern, und erzählt im Gespräch mit Sebastian Ritterbusch, wie er didaktische Konzepte für den Mathematikunterricht erforscht und aktiv erprobt. Die Frage nach Verbesserung des Mathematik-Unterrichts ist sehr aktuell: Die OECD-Studie zu Geschlechtsunterschieden in der Schule hat gerade in Mathematik Verbesserungspotential aufgezeigt, denn viele geben Mathe auf, weil sie nachweislich fälschlich glauben, sie könnten es nicht. Der zentrale Begriff ist hier die Selbstwirksamkeitserwartung, die insbesondere in Naturwissenschaften und Mathematik durch gesellschaftliche Einflüsse stark geprägt ist. Die Erforschung neuer Lehrmethoden kann aber nicht den Ersatz der bisherigen und erprobten Konzepte zum Ziel haben: So sind selbst vermeintlich alte Übungen zum Kopfrechnen und zur schriftlichen Division auch heute noch überaus wichtige Hilfen zur Vermittlung von Algorithmen, Stellenwertsystemen und auch zur Vorbereitung auf ein Studium. Das Ziel muss sein, den Fundus möglicher Vermittlungsformen zu bereichern, und für verschiedene Konzepte bessere Kombinationen der Verfahren zu finden. Ein nützliches neues Werkzeug ist die Tabellenkalkulation, mit der beispielsweise Würfelexperimente und Simulationen im Unterricht interaktiv erfahrbar gemacht werden können. Ebenso können Dynamische Geometriesysteme den Zugang zur Konstruktion und Analytischer Geometrie, wie beispielsweise den Satz des Thales, deutlich vereinfachen. Die Software GeoGebra ist ein solches System, das insbesondere auch unterschiedliche Darstellungen und Analyse der Konstruktionen ermöglicht. Leider ist es zu Zeit noch nicht möglich, dass in Klassen jederzeit an jedem Platz ein Rechner zum Einsatz interaktiver Experimente vorhanden ist. Aber auch an einem interaktiven Whiteboard können die Methoden durchgeführt werden. Die technische Ausstattung ist aber nur ein kleiner Schritt zur Einführung neuer Werkzeuge in den Unterricht, auch die Lehrerinnen und Lehrer müssen die Kompetenzen zum Einsatz der neuen Medien erlernen. Hier müssen die pädagogischen Hochschulen den Lehramtsstudierenden den Weg bereiten, damit das Lehrpersonal zu Beginn und auch in ihrer langen Lehrzeit für den Stand und die Entwicklung der Technik vorbereitet ist. Auch Wissensmanagement in der Form von Wikis haben in Schulen Einzug gehalten, so setzen Maria Eirich und Andrea Schellmann auf ein Schulwiki am Regiomontanus-Gymnasium Haßfurt und Lernpfade zum interaktiven Mathematik-Unterricht. Auch Schülerinnen und Schüler können hier selbst Quiz-Aufgaben erstellen. Michael Gieding und Andreas Schnirch haben für Geometrie-Vorlesungen an der PH Heidelberg ein Geometrie-Wiki auf dieser Technologie erstellt, das auch weiterhin für Lehrveranstaltungen für Lehramtsstudierende genutzt wird. Eine Einführung in die frühen interaktiven Elemente am CMS der Fakultät für Mathematik sind auf der Fragebogen-Seite mit einer Vielzahl von Beispielen zu finden. Gerade in Mathematik stellt die Einbindung digitaler Medien eine gewisse Hürde dar, da Formeln, Beweise, Algorithmen und Konstruktionszeichnung nicht leicht digitalisierbar sind- auch wenn das Textsatz-System LaTeX oder LyX im mathematischen Bereich mit perfektem Druckbild für fast alles verwendet werden kann, so muss man es erst erlernen- beispielsweise mit der l2kurz-Anleitung. Das Austauschen von abfotografierten Seiten ist da häufig deutlich effektiver. Dabei ein solcher Austausch zwischen den Lernenden sehr zu begrüßen, da es zum einen die gemeinsame Konstruktion von Lösungswegen begünstigt, aber auch die angehenden Lehrenden auf die Nutzung der Medien trainiert. Wichtig sind niederschwellige Zugänge und die Möglichkeit zu anonymen Beiträgen, da nur so das Lernen aus Fehlern ermöglicht wird. Im Flipped Classroom wird der Prozess der interaktiven Auseinandersetzung mit dem Lernstoff, der traditionell zu Hause erst bei den Hausaufgaben auftritt, in den Unterricht gebracht, und der herkömmliche Frontal-Unterricht aus dem Klassenzimmer verbannt. Dazu erhalten die Schülerinnen und Schüler oder die Studierenden zur Vorbereitung ein Video, in dem das grundsätzliche Verfahren erklärt wird. Die Unterrichtsstunde kann dann mit einer Fragerunde zum Videomaterial starten, gefolgt von einigen Aufgaben, die vom Plenum in Gruppenarbeit bearbeitet werden sollen. Hier werden Probleme und Fragen offensichtlich, die vom Lehrenden oder gemeinsam in einer Diskussion erörtert werden können. Anschließend könnte sich ein Hörsaal- oder Klassenzimmerspiel anschließen, das sowohl auflockert, als auch das Thema verfestigt. Dass besondere Ereignisse den Lernerfolg verbessern können, wurde auch beim Thema >Gestern hab ich noch Zeit genug< im Methodisch-Inkorrekt Podcast Folge 43 besprochen. Auch wenn es nicht immer außerordentliche Ereignisse geben kann, so ist eine sinnvolle Abwechslung der Lehrmethoden sicher zuträglich zur Verbesserung des Unterrichts. Neben der Frage zur zeitlichen Planung des Unterrichts sind auch Fragen innerhalb der Mathematik eine Untersuchung auf mögliche Vermittlungsmethoden interessant: Die Gaußsche Summenformel ist nicht nur wichtig zur Berechnung der Anzahl der Spiele in einer Fußball-Liga, sondern auch ein schönes Beispiel zur verschiedene mathematische Beweisverfahren. Die Formel kann durch vollständige Induktion bewiesen werden, ein anderer Ansatz ist die Verwendung von Dreieckszahlen zu einem ebenso korrekten ikonischen Beweis der Summenformel. Einen wichtigen Stellenwert hat auch die Haltung der Lehrperson: Anstatt zu demoralisieren, müssen die Lernenden in ihrem Lernprozess unterstützt und bei Bedarf geleitet werden. Dazu gehört auch die Anpassung der Komplexität an die unterschiedlichen Kenntnisse der Lernenden- eine fast unmögliche Aufgabe angesichts großer Unterschiede in den Vorkenntnissen. Eine Möglichkeit sind Angebote für optionale Übungsgruppen, oder Zusatzangebote für weitergehende Fragen. Ideal sind jedoch natürlich differenzierende Aufgaben, die von allen Lernenden je nach ihrem Kenntnisstand hinreichend und unterschiedlich umfangreich beantwortet werden können. Ein Beispiel ist hier die Aufgabe zu den Pythagoreischen Zahlentripeln, die sehr knapp, aber auch sehr weitreichend beantwortet werden kann. Eine andere interessante Frage steckt im Münzproblem, die man bis zur Frage der kleinsten Anzahl von Münzen zur Rückgabe aller Geldbeträge von 1-99 Cent beantworten kann (Optimal sind acht Münzen in vier möglichen Variationen: zB 1+1+2+5+10+10+20+50 oder 1+2+2+5+10+20+20+50). Die Frage der Evaluation von Unterrichtsmethoden wie dem Flipped Classroom ist leider nicht einfach zu beantworten: Es ist kaum möglich zwei Gruppen parallel und voneinander unbeeinflusst unterschiedlich zu unterrichten. Bei einer Evaluation zwischen verschiedenen Jahrgängen konnte ein besseres Abschneiden bei Prüfungen nicht sicher nachgewiesen werden, jedoch ist war das subjektive Empfinden der Studierenden gegenüber den neuen Methoden ausgesprochen positiv. Malte Persike hat entsprechende Ergebnisse erhalten, u.a. beim MOOC zur Wahrscheinlichkeitsrechnung, stellt aber auch zur Diskussion, dass bei mit herkömmlichen Methoden weniger erfolgreichen Dozenten die neue Methoden deutlich bessere Ergebnisse erzielen könnten. Bei der Umstellung auf Flipped Classroom-Konzepte ist die Videoerstellung oft nicht sehr aufwendig, da hier abgefilmte frühere Veranstaltungen in Frage kommen können. Dafür ist die Umstellung und die Planung des neuen Unterrichts oftmals deutlich aufwendiger, wenn man eine Stunde zum ersten Mal durchführt. Anders sieht es bei einem Massive Open Online Course, kurz MOOC, aus, für den Videos deutlich aufwendiger und in kürzerer Form produziert werden. MOOCs sind besonders durch Sebastian Thrun bekannt geworden, als er eine Vorlesung zur künstlichen Intelligenz online zur Verfügung stellte, an der etwa 160'000 Studierende teilnahmen. In der Regel werden Videos mit vorlesungsartigen Inhalten wöchentlich online gestellt, zu denen die Teilnehmer regelmäßig Aufgaben gestellt bekommen. Durch Verfügbarkeit im Internet können sehr viele an diesen Kurs teilnehmen, und durch die Verwendung offener Technologien und Zugänge ist die Teilnahme sehr niederschwellig und spricht viele Interessenten an. An der PH Heidelberg wurde der Mathe-MOOC Mathematisch Denken von Christian Spannnagel, Michael Gieding, Lutz Berger und Martin Lindner ins Leben gerufen, der das MOOC-Konzept nicht ganz klassisch umgesetzt hat. Viel mehr wurde ein Schwerpunkt auf Mathematikdidaktik gelegt: Statt einem festen Wechsel von Vorlesung und Übung wurden einführende experimentelle Einheiten eingesetzt, bei denen die Teilnehmenden schon im Vorfeld Ihre eigenen Erfahrungen mit dem Thema machen konnten. Die Bearbeitung der Aufgaben und der Vergleich der Lösungen erfolgte dann in öffentlichen Foren- eine abschließende Prüfung war in diesem MOOC nicht vorgesehen, sondern möglichst vielen einen Einstieg in die mathematische Denkweise ermöglichen. Die Teilnehmenden können sich selbst als Kiebitze, Anpacker und Formalisierer bezeichnen, auch von Aufgabe zu Aufgabe unterschiedlich- die Kiebitze sind hauptsächlich passive Zuschauer, wogegen die Anpacker die Lösungen aktiv, beispielsweise ikonisch, erarbeiten wollen. Die Formalisierer suchen schließlich die exakte mathematische Beschreibung und symbolische Lösung der Aufgaben. Diese Differenzierung ermöglicht eine Klarstellung der eigenen Teilnahmeabsicht und vereinfacht durch die Vorgabe verschiedener Ansätze den Zugang in den jeweiligen Nutzungsszenarien. MOOCs können und sollten herkömmliche Präsenzveranstaltungen nicht ersetzen, sondern die Nutzung wie beim Flipped Classroom-Konzept die Qualität der Präsenzveranstaltungen verbessern. Ausgesprochen sinnvolle Beispiele zum Einsatz von MOOCs sind Brückenkurse vor Studienbeginn, wo noch nicht alle Studierende am Studienort sind, oder in der Weiterbildung für Berufstätige. Der Mathe-MOOC Mathematisch Denken findet aktuell jedes Semester statt, und wer mitmachen möchte, kann jeweils Anfang April oder Anfang Oktober einsteigen. Die Kurse werden auch kontinuierlich weiter entwickelt. So werden nun mit Christian Freisleben-Teutscher Improvisationsmethoden eingebunden, um die gegenseitige Interaktion zwischen den Teilnehmenden zu fördern. Schon seit Beginn des Mathe-MOOCs sind auch szenische Darstellungen sehr erfolgreicher Teil der Darstellung, und dienen der Motivation und Auflockerung der manchmal trockenden Mathematik. So tritt Christian Spannagel oft als Dunkler Lord auf, der auf seine besondere Weise die Mathematik erklärt. Wie es schon Jean-Pol Martin formulierte, haben Professoren die Verantwortung neue Wege zu gehen, um für die Gesellschaft auch riskantere Wege einzuschlagen. Auch am KIT werden erfolgreich MOOCs angeboten, und der MOOC gegen Chronisches Aufschieben wurde vor kurzem mit dem Bildungsmedienpreis digita ausgezeichnet. Ein weiterer neuer Zugang ist die Gamification, bei der spielerische Elemente in spielfremde Bereiche eingeführt werden. Dies kann durch die Zuteilung von Punkten, Leveln oder Abzeichen bzw. Badges erfolgen, und dies kann auch in der Hochschullehre eingesetzt werden. Die Wahl eines Kontexts hat sich aber als kritisch herausgestellt: Wenn die Lernenden sich nicht mit dem Spiel identifizieren können, ist kaum ein Erfolg zu erwarten. Nando Stöcklin und Nico Steinbach entwickelten das erfolgreiche System QuesTanja, mit den Schülerinnen und Schüler mit Tablets selbstständig Mathematik erlernen können. Die Forschung richtet sich hier auf die Konzepte des Design-based Research, sie konzentriert sich also darauf die Methode zu entwickeln und iterativ und zyklisch zu verbessern. Auch zum Erlernen des Programmierens haben sich spielerische Konzepte bewährt, ein Beispiel dafür ist die Plattform Scratch und ScratchJr, oder auch Lightbot. Diese Lernprinzipien gehen auf Seymour Papert zurück, der schon mit der Programmiersprache Logo den Grundstein zu erziehungsorientierten Programmiersprachen gelegt hat. Die Logo-Programmiersprache gab es als Schildkrötengrafik auch schon im NDR-Klein-Computer. Eine interessante Frage im Umgang mit neuen Medien in Lehre und Wissenschaft ist die Zitierbarkeit der Angebote. Auf der einen Seite geben sich neue Nutzungsmöglichkeiten durch direkte Links an bestimmte Zeitpunkte, jedoch sind Zitate auf Videos, Audiodateien und Internetseiten noch nicht in der wissenschaftlichen Literatur etabliert. Neue Ansätze zur Vortragsaufzeichnung beim KonScience Podcast werden diskutiert. Ein wichtiger Ansatz ist auch die Vergabe von DOI-Nummern für digitale Medien, wie es auch im Open Science Radio Podcast angesprochen wurde. Letztendlich kann man bei der Erstellung von Videos für den Unterricht nicht zu viel Perfektionismus an den Tag legen, wie es auch schon Aaron Sams formulierte: "Do you need it perfect, or do you need it by Tuesday?" Literatur und Zusatzinformationen
| |||||||||||||||||||
| 16 Apr 2015 | Erdrutsche | 00:37:28 | |||||||||||||||||
Katharina Elsen ist für 6 Monate aus Bologna im Rahmen eines Forschungsaufenthalts nach Karlsruhe gekommen. In Ihrer Forschungsgruppe zur numerischen Geophysik sind Tsunamis im Mittelmeerraum, wie beispielsweise im Raum von Italien und der Türkei, das Hauptforschungsgebiet. Ein Auslöser für Tsunamis sind Erdbeben, aber auch Erdrutsche können der Grund für die großen Wasserwellen sein, die dann sogar eine globale Auswirkung haben können. Im Varjont-Tal kam es 1963 nach dem Aufstauen eines Stausees zu einem Landrutsch. Dieser führte zu einer Tsnuamiwelle im Stausee, die in ihrer Größe weit unterschätzt wurde, und zur schrecklichen Tragödie von Langarone führte. Solche Vorgänge können natürlich auch in Küstengebieten auftreten und die gegenüberliegenden Küsten gefährden. Im Gegensatz zu sehr plötzlichen seismischen Aktivitäten können Landrutsche weit langfristigere Vorgänge sein. Auch können die sich bewegenden Landmassen aus beweglichem Schlamm oder feinem Geröll bestehen oder aus eher festen Bestandteilen. Dies beeinflusst stark die möglichen Modelle, und Katharina Elsen beschreibt im Gespräch mit Gudrun Thäter ihre Modelle und Forschung zu Landrutschen von Bergabschnitten, die sich eher wie ein Festkörper als wie ein Fluid verhalten. Die Landmassen werden in einige Festkörper-Masseblöcke aufgeteilt, die jeweils Massenzentren bzw. Baryzentren besitzen und deren Berandung bekannt ist. Daraus wird die individuelle Bewegung der Blöcke modelliert, wie auch die gegenseitige Beeinflussung auf verschiedene Arten. Letztlich wird dann untersucht, wie die Blöcke letztlich durch Geschwindigkeit und Form auf das Wasser wirken, um bessere Aussagen über resultierende Wellenhöhe treffen zu können. Der erste Schritt zur Simulation ist die Zerlegung der gleitenden Oberflächen in Dreiecke, und dann wird die Bewegung der einzelnen Massepunkte für das vereinfachte Modell durch die klassische Newtonsche Mechanik zunächst exakt berechnet. Für die Beeinflussung der Massepunkte zueinander werden verschiedene approximierende Modelle erforscht, und Parameter entsprechend den Beobachtungen identifiziert. Die Ansätze und Modelle fließen in eine Software zur Erdrutschsimulation, die auch im Bereich der Reibungsmodelle überarbeitet wurde: Da auf triangulisierten Oberflächen alle Funktionen und Eigenschaften dort bisher nur in linearisierter Form auftreten, können höhere Ableitungen nur über erweiterte Modelle approximiert werden. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 30 Apr 2015 | Strukturoptimierung | 00:50:26 | |||||||||||||||||
Peter Allinger und Nick Stockelkamp optimieren bei der Dassault Systèmes in Karlsruhe Formen, Strukturen und Strömungen im Bereich des Maschinenbaus. Anwendungsbeispiele reichen vom Zahnimplantat bis zum Schiffsdiesel und typische Optimierungskriterien sind Gewicht, Fertigungskosten und Haltbarkeit. Dabei hat sich der Fokus von einfachen Fragestellungen wie der Durchbiegung hin zu komplexen Fragestellungen wie der Geräuschentwicklung. In der Fluid-Optimierung geht es unter anderem um die Reduzierung von Druckverlusten, der Vermeidung von Turbulenzen oder auch Verbesserung von Wärmetauschern, beispielweise unterstützt durch den Löser OpenFOAM. Dabei gibt es unterschiedliche Vorhegensweisen: Man kann entweder die Veränderung der Objekte durch Hinzufügen oder Abziehen von Material hervorrufen, oder man berechnet die Sensitivität der Zielgröße bezüglich Veränderungen an den Oberflächen. Der mögliche Design-Raum wird in vielen Anwendungen mit der Finite-Elemente-Methode diskretisiert, um zu einem lösbaren Problem zu gelangen, wobei Strömungen oft mit Finite-Volument-Verfahren gelöst werden. Die zentrale Frage ist jedoch, wann man ein Bauteil als optimal bezeichnen kann. Hier hat Prof. Eckart Schnack in den 70er Jahren den Ansatz beschrieben, dass eine gleichmäßige Spannungsverteilung eines beanspruchten Bauteils ein optimales Bauteil auszeichnen kann. Im Fall von strukturmechanischen Belastungen gibt es für diesen Optimalitätsbegriff iterative Löser, jedoch sind Fragestellungen im Umfeld von Eigenwertprobleme noch ein offenes Forschungsgebiet. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 07 May 2015 | Waves | 00:48:10 | |||||||||||||||||
Prof. Enrique Zuazua is a Distinguished Professor of Ikerbasque (Basque Foundation for Science) and Founding Scientific Director at the Basque Center for Applied Mathematics (BCAM), which he pushed into life in 2008. He is also Professor in leave of Applied Mathematics at the Universidad Autónoma de Madrid (UAM) and a Humboldt Awardee at the University of Erlangen-Nuremberg (FAU) as well. He was invited by the PDE-group of our Faculty in Karlsruhe to join our work on Wave Phenomena for some days in May 2015. In our conversation he admits that waves have been holding his interest since his work as a PhD student in Paris at the Université Pierre-et-Marie-Curie in the world famous group of Jacques-Louis Lions. Indeed, waves are everywhere. They are visible in everything which vibrates and are an integral part of life itself. In our work as mathematician very often the task is to influence waves and vibrating structures like houses or antennae such that they remain stable. This leads to control problems like feedback control for elastic materials. In these problems it is unavoidable to always have a look at the whole process. It starts with modelling the problem into equations, analysing these equations (existence, uniqueness and regularity of solutions and well-posedness of the problem), finding the right numerical schemes and validating the results against the process which has been modelled. Very often there is a large gap between the control in the discrete process and the numerical approximation of the model equations and some of these differences are explainable in the framework of the theory for hyperbolic partial differential equations and not down to numerical or calculation errors. In the study of Prof. Zuazua the interaction between the numerical grid and the propagation of waves of different frequencies leads to very intuitive results which also provide clear guidelines what to do about the so-called spurious wave phenomena produced by high frequencies, an example of which is shown in this podcast episode image. This is an inherent property of that sort of equations which are able to model the many variants of waves which exist. They are rich but also difficult to handle. This difficulty is visible in the number of results on existence, uniqueness and regularity which is tiny compared to elliptic and parabolic equations but also in the difficulty to find the right numerical schemes for them. On the other hand they have the big advantage that they are best suited for finding effective methods in massively parallel computers. Also there is a strong connection to so-called Inverse Problems on the theoretical side and through applications where the measurement of waves is used to find oil and water in the ground, e.g (see, e.g. our Podcast Modell004 on Oil Exploration). Prof. Zuazua has a lot of experience in working together with engineers. His first joint project was shape optimization for airfoils. The geometric form and the waves around it interact in a lot of ways and on different levels. Also water management has a lot of interesting and open questions on which he is working with colleagues in Zaragoza. At the moment there is a strong collaboration with the group of Prof. Leugering in Erlangen which is invested in a Transregio research initiative on gasnets which is a fascinating topic ranging from our everyday expectations to have a reliable water and gas supply at home to the latest mathematical research on control. Of course, in working with engineers there is always a certain delay (in both directions) since the culture and the results and questions have to be translated and formulated in a relevant form between engineers and mathematicians. In dealing with theses questions there are two main risks: Firstly, one finds wrong results which are obviously wrong and secondly wrong results which look right but are wrong nonetheless. Here it is the crucial role of mathematicians to have the right framework to find these errors. Prof. Zuazua is a proud Basque. Of the 2.5 Mill. members of the basque people most are living in Spain with a minority status of their culture and language. But since the end of the Franco era this has been translated into special efforts to push culture and education in the region. In less than 40 years this transformed the society immensely and led to modern universities, relevant science and culture which grew out of "nothing". Now Spain and the Basque country have strong bonds to the part of Europe on the other side of the Pyrenees and especially with industry and research in Germany. The Basque university has several campuses and teaches 40.000 students. This success could be a good example how to extend our education system and provide possibilities for young people which is so much a part of our culture in Europe across the boundaries of our continent. | |||||||||||||||||||
| 11 Jun 2015 | L-Funktionen | 00:59:51 | |||||||||||||||||
Eine alte Fragestellung lautet, was die Summe der Kehrwerte aller natürlicher Zahlen ist. Mit anderen Worten: existiert der Grenzwert der Harmonischen Reihe Eine verwandte Fragestellung zur harmonischen Reihe lautet: Wie steht es um den Wert von Eine ähnliche Reihe ist Ihr Wert läßt sich elementar bestimmen. Dies war lange bekannt, und das Basel-Problem war ungleich schwieriger: Es blieb fast einhundert Jahre lang ungelöst. Erst Leonhard Euler löste es 1741: Die Riemann'sche | |||||||||||||||||||
| 25 Jun 2015 | Steganographie | 01:40:04 | |||||||||||||||||
Seit 2002 veranstaltet der Entropia e.V. in Karlsruhe jährlich die Gulaschprogrammiernacht, das ist ein mehrtägiger Kongress, wo Nerds, Häcksen und Maker ihre Projekte vorstellen, Erfahrungen austauschen und Vorträgen lauschen. Die GPN15 fand Anfang Juni 2015 im ZKM und der HfG Karlsruhe statt. Hier hat Marius Musch in einem Vortrag eine Einführung in die Steganographie gegeben, und spricht nun mit Sebastian Ritterbusch im Podcast. Bei der Steganographie geht es darum, eine geheime Nachricht so zu versenden, dass niemand außer dem gewünschten Empfänger die Existenz dieser Nachricht überhaupt vermutet. Der Begriff kommt aus dem griechischen und bedeutet in etwa "geheimes Schreiben". So wurden schon in der Antike erste simple Formen der Steganographie verwendet. Statt wie üblich die Nachricht in der Wachs auf einer Wachstafel zu kratzen, wurde die geheime Nachricht in das Holz darunter geritzt und wieder Wachs darüber gegossen. Anschließend konnte eine harmlose Nachricht in das Wachs geschrieben werden und die geheime Nachricht war verdeckt darunter. Mit der Zeit wurden die Verfahren dann raffinierter, so wurde im Zweiten Weltkrieg aus einem japanischen Kriegsgefangenenlager eine scheinbar harmlose Postkarte verschickt. Liest man aber nur die ersten beiden Wörter jeder Zeile ergibt sich ein völlig neues Bild und es werden die Truppenverluste der Amerikaner kommuniziert. In in einem anderen Fall vereitelte amerikanische Kriegsgefangene Jeremiah Denton die Propagandaversuche in Vietnam während des Kalten Krieges. Während eines TV-Interviews blinzelte er wiederholt das Wort T-O-R-T-U-R-E in Morsecode. In der heutigen Zeit ist es natürlich naheliegend die Steganographie in der digitalen statt der analogen Welt einzusetzen. So kann man zum Beispiel schon in (Plain-)Text eine geheime Nachricht verstecken. Viele Texteditoren zeigen standardmäßig Leerzeichen und Tabs am Zeilenende (trailing whitespace) nicht an. Dies macht sich das Tool SNOW (steganographic nature of whitespace) zu nutze, um geheime Nachrichten zu verstecken, oder man schreibt gleich komplette Programme in der etwas verrückten Programmiersprache Whitespace. Deutlich verbreiteter und effektiver ist es aber als Tarn-Medium (das so genannter Cover) ein Bild zu nehmen. Bilder haben viele nützliche Eigenschaften, insbesondere dass geringe Änderungen für das menschliche Auge unsichtbar bleiben. Aber auch ihre Größe ist vorteilhaft da ein Bild leicht um den Faktor 1000 größer ist, als die darin zu versteckende Nachricht. Bei einem Grauwertbild wird typischerweise ein Byte pro Pixel verwendet, also die Helligkeit jedes Bildpunktes wird durch einen Wert zwischen 0 für Schwarz und 255 für Weiß repräsentiert. Dieses Byte besteht wiederum aus 8 Bits, zum Beispiel der Folge 11110000 für den Wert 120. In der Steganographie kann man sich zu Nutze machen, dass das hinterste Bit (least significant bit) nur sehr wenig zum eigentlichen Farbwert beträgt. Es entscheidet nur ob die Zahl gerade oder ungerade ist und wenn der Wert geändert wird, fällt einem Menschen dieser geringe Helligkeitsunterschied gar nicht auf. Somit kann man nun seine geheime Nachricht von den ASCII-Werten in Binärzahlen konvertieren und anschließend in den least significant Bits (LSBs) einbetten. Man braucht also 8 Pixel pro Buchstabe. Weitere Verfahren gibt es auf Basis spezieller Eigenschaften von Datenformaten wie GIF, PNG oder JPEG. Bei der Steganographie gibt es aber auch einiges zu beachten. Besonders wichtig ist es die Nachricht vor dem Einbetten zu verschlüsseln. Zum einen kann uns ein Angreifer, der das Verfahren kennt und die Nachricht extrahiert, sie trotzdem nicht lesen. Zum anderen lässt sich ein gut verschlüsselter Ciphertext nicht von echtem Zufall unterscheiden, um Angriffe zu erschweren. Hat man aber Zugriff auf das Orginalbild, so wird der Unterschied und damit die Nachricht offensichtlich- hier sind besonders umgekehrte Bildersuchen hilfreich. Im realen Einsatz sind meist Wasserzeichen, die Verfahren der Steganographie verwenden. Anders als bei der Steganographie, wo das Cover völlig irrelevant für die geheime Nachricht war, bezieht sich bei den Wasserzeichen die versteckte Nachricht auf das Cover. So bestätigt das Wasserzeichen auf einem Geldschein die Authentizität eben dieses Scheines. Es gibt aber auch Wasserzeichen die lange unbekannt waren. Zum Beispiel gibt es einige Drucker bekannter Hersteller, die in die ausgedruckten Seiten ein kaum sichtbares gelbes Punktemuster einbauen. In diesem Wasserzeichen steht sowohl das Datum des Druckes als auch die Seriennummer des Druckers. Auf Geldscheinen gibt es gelben Punkte in der EURion-Konstellation, die von Kopierern, Scannern und Software erkannt werden. Aber auch Spieler von Onlinerollenspielen wie World of Warcraft sind vor Wasserzeichen nicht sicher. So wurde 2012 in einem Forum bemerkt, dass die Screenshots aus dem Spiel per Wasserzeichen den Accountname und die Server-IP des Spielers beinhalten. Allerdings hinterlässt die Steganographie auch immer zwangsweise ihre Spuren, da das Bild manipuliert werden muss. Um die oben beschriebene LSB-Methode durch eine Steganalyse zu erkennen, reicht es sich das Histogramm des Bildes anzuschauen, denn durch das Verfahren ergeben sich treppenartige Abstufungen. Dies wiederum versucht das Tool Outguess zu vermeiden, indem es die LSB Änderungen geschickt über die Datei verteilt und das Histogramm unauffällig bleibt. Beliebte Angriffsmethoden sind auch die Autokorrelation und die FFT über das Wiener-Chintschin-Theorem, womit eine sehr effiziente Berechnung möglich wird. Das aktuelle Folgenbild des Podcasts zeigt ein Bild mit steganographisch versteckter Nachricht, das Marius für einen Capture the Flag-Wettbewerb auf der GPN14 im letzten Jahr erstellt hatte und jetzt erklärt. Auch auf der GPN15 gab es dieses Jahr wieder einen Capture the Flag Wettbewerb, veranstaltet von den Squareroots aus Mannheim und KITCTF aus Karlsruhe. Auch dieses Jahr lag der Fokus auf IT-Sicherheit: Die teilnehmenden Teams erhalten eine virtuelle Maschine (Vulnbox) mit mehreren verwundbaren Diensten, die sie analysizeren, die Ausnutzbarkeit prüfen und letztlich absichern sollen. Ein zentraler Gameserver verteilt sogenannte Flaggen an alle Teams, das sind lange zufällige Zeichenketten. Diese Flaggen gilt es zu verteidigen und durch Finden und Ausnutzen von Sicherheitslücken in den Diensten der anderen Teams zu stehlen und für Punkte beim Veranstalter einzureichen. Beim CTF auf der GPN15 gab es 11 teilnehmende Teams, die sich über einen Zeitraum von 5 1/2 Stunden insgesamt 7600 Flaggen gestohlen haben. Wer mehr über CTFs erfahren möchte, sollte insbesondere den CTF Field Guide lesen. Eine Übersicht über anstehende Veranstaltungen und die verschiedenen Teams findet man unter CTF Time. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 18 Jun 2015 | Spielcomputer | 02:02:30 | |||||||||||||||||
Seit 2002 veranstaltet der Entropia e.V. in Karlsruhe jährlich die Gulaschprogrammiernacht, das ist ein mehrtägiger Kongress, wo Nerds, Häcksen und Maker ihre Projekte vorstellen, Erfahrungen austauschen und Vorträgen lauschen. Die GPN15 fand Anfang Juni 2015 im ZKM und der HfG Karlsruhe statt, und zog diesmal auch Mathe-Begeisterte an: Florian Gilges ist mit dem Life Science Lab als Schüler nach Karlsruhe gekommen, und will unter anderem Näherungen an die Kreiszahl Zunächst ist die Kreiszahl Um nun eine Näherung für Pi zu berechnen, lassen sich verschiedene Verfahren verwenden: Ein Kreis wird gezeichnet und Umfang und Durchmesser gemessen, das Verhältnis ist dann eine Näherung an Pi. Eine andere Möglichkeit ist die Berechnung durch eine Winkelfunktion: Der Arkustangens hat bei 1 den Wert Die Berechnung will Florian in Minecraft durchführen, und baut sich dafür einen Rechner innerhalb dieses Spiels. Aber wie kann ein einfaches Spiel so etwas bieten? Schließlich ist Minecraft nur eine Nachahmung unserer Welt mit ganz natürlichen Ressourcen. So bietet eine Minecraft-Welt verschiedene Vegetations- und Klimazonen und verschieden Landschaften und Umgebungen, wie z.B. Laubwälder, Nadelwälder, Steppen, Wüsten, Schneegebiete, uvm. Es gibt jedoch auch Stoffe, die es in unserer Welt nicht gibt: Einer davon ist Redstone. Dieser besondere Stoff kann in Höhlen tief unter der Erde als Erz gefunden werden und gibt abgebaut ein Pulver, das ähnliche Eigenschaften, wie elektrische Leitungen hat. Aus Redstone-Pulver und weiteren Materialien, die man in der Welt findet, lassen sich Logikelemente bauen: Inverter, Verstärker, Verzögerer und Vergleicher. Diese Basiselemente können vom Spieler in die Welt gebaut und zu großen Schaltungen zusammengesetzt werden. Angefangen bei einfachen Speichern und Signalstärkespeichern (Redstone-Energie hat 16 Stufen von 0 bis 15), bis hin zu Logikgattern, wie UND-Gatter, XOR-Gatter und Flip-Flops. Kurzum lassen sich mit den Basiselementen alle Komponenten für einen Computer zusammenstellen, aber auch einfachere Dinge, wie Code-Schlösser und Tür-Steuerungen sind möglich. Doch so einfach, wie es nun erscheint, ist es nicht, denn jedes Basiselement hat eine Verzögerung von mindestens einer Zehntel- bis vier Zehntelsekunden. Das bedeutet, dass der Computer sehr langsam wird und Berechnungen sehr aufwendig werden. Deshalb ist Optimierung sehr wichtig, indem an jeder Stelle die Bauteile effizienter gemacht werden und die Mathematik zur Berechung ebenfalls (für den Computer) effizienter gestaltet wird. Hier konnte Florian das XOR-Gatter und den Programm-Zähler aus Halbaddierern und Volladdierern durch intelligente Kniffe deutlich beschleunigen. Eine weitere Möglichkeit besteht auch in der Nutzung von redundanten Binärdarstellungen, die bei einer großen Anzahl von Additionen große Geschwindigkeitsvorteile bringen können. Neben der Optimierung der Hardware ist auch die Optimierung der Software wichtig, was zur Mathematik zurückführt: Berechnungen wie Multiplikationen, Potenzen oder Wurzeln sind auf Logikebene komplizierte Operationen, auch wenn unsere Taschenrechner die Aufgaben in Sekundenbruchteilen lösen. Der einfachste Weg für die Multiplikation ist, dass man eine Additionskette bildet: Komplizierter sind dann schon Wurzeln. Diese lassen sich nicht so leicht berechnen, wie eine Addition oder Multiplikation. Ein mögliches Näherungsverfahren ist das Heron-Verfahren. Es gibt jedoch auch das schriftliche Wurzelziehen, das im Binärsystem leicht zu implementieren ist. Florian hat sich diese Techniken aus Videos wie dem Youtube-Kanal Schoolseasy selbst angelernt. | |||||||||||||||||||
| 02 Jul 2015 | Acoustic Scattering | 00:40:39 | |||||||||||||||||
Prof. Francisco Sayas from the Department of Mathematical Sciences of the University of Delaware in Newark has been visiting our faculty in June 2015. He is an expert in the simulation of scattering of transient acoustic waves. Scattering is a phenomenon in the propagation of waves. An interesting example from our everyday experience is when sound waves hit obstacles the wave field gets distorted. So, in a way, we can "hear" the obstacle. Sound waves are scalar, namely, changes in pressure. Other wave types scatter as well but can have a more complex structure. For example, seismic waves are elastic waves and travel at two different speeds as primary and secondary waves. As mathematician, one can abandon the application completely and say a wave is defined as a solution of a Wave Equation. Hereby, we also mean finding these solution in different appropriate function spaces (which represent certain properties of the class of solutions), but it is a very global look onto different wave properties and gives a general idea about waves. The equations are treated as an entity of their own right. Only later in the process it makes sense to compare the results with experiments and to decide if the equations fit or are too simplified. Prof. Sayas startet out in a "save elliptic world" with well-established and classical theories such as the mapping property between data and solutions. But for the study of wave equations, today there is no classical or standard method, but very many different tools are used to find different types of results, such as the preservation of energy. Sometimes it is obvious, that the results cannot be optimal (or sharp) if e.g. properties like convexity of obstacles do not play any role in getting results. And many questions are still wide open. Also, the numerical methods must be well designed. Up to now, transient waves are the most challenging and interesting problem for Prof. Sayas. They include all frequencies and propagate in time. So it is difficult to find the correct speed of propagation and also dispersion enters the configuration. On the one hand, the existence and regularity together with other properties of solutions have to be shown, but on the other hand, it is necessary to calculate the propagation process for simulations - i.e. the solutions - numerically. There are many different numerical schemes for bounded domains. Prof. Sayas prefers FEM and combines them with boundary integral equations as representative for the outer domain effects. The big advantage of the boundary integral representation is that it is physical correct but unfortunately, it is very complicated and all points on the boundary are interconnected. Finite Elements fit well to a black box approach which leads to its popularity among engineers. The regularity of the boundary can be really low if one chooses Galerkin methods. The combination of both tools is a bit tricky since the solver for the Wave Equations needs data on the boundary which it has to get from the Boundary element code and vice versa. Through this coupling it is already clear that in the coding the integration of the different tools is an important part and has to be done in a way that all users of the code which will improve it in the future can understand what is happening. Prof. Sayas is fascinated by his research field. This is also due to its educational aspect: the challenging mathematics, the set of tools still mainly unclear together with the intensive computational part of his work. The area is still wide open and one has to explain mathematics to other people interested in the results. In his carreer he started out with studying Finite Elements at the University in Zaragoza and worked on boundary elements with his PhD-supervisor from France. After some time he was looking for a challenging new topic and found his field in which he can combine both fields. He has worked three years at the University of Minnesota (2007-2010) and decided to find his future at a University in the U.S.. In this way he arrived at the University of Delaware and is very satisfied with the opportunities in his field of research and the chances for young researchers. Literature and additional material
| |||||||||||||||||||
| 09 Jul 2015 | Zweibeiner | 00:36:37 | |||||||||||||||||
Wie bringt man einem Roboter das Gehen bei? Cornelius Kuhs hat sich dieser Frage am Humanoiden Fünf-Segment-Läufer am Institut für Technische Mechanik gestellt, und hat die Bewegungen am Modell von Differentialgleichungen auf die Energieeffizienz des Bewegungsablaufs studiert. Die Energieeffizienz bezieht sich hier auf die spezifischen Transportkosten, das ist hier die aufgebrachte Energie geteilt durch das Produkt von Gewicht und zurückgelegter Distanz. Die Bewegungsabläufe sind jedoch nicht durch analytisches Lösen der Differentialgleichungen des Modells zu bestimmen, hier wurden verschiedene Ansätze ausgetestet, die dann mittels mathematischer Optimierung auf einen möglichst geringen Energieverbrauch verbessert werden. Dabei sind viele physikalische Randbedingungen, wie der Position des Bodens, und technische Bedingungen, die beispielsweise das Umknicken des Kniegelenks verhindern, schon im Modell eingebaut. Darüber hinaus gibt es aber auch weitere Eigenschaften und Einschränkungen, die verschiedene Lösungen mehr oder weniger nützlich erscheinen lassen. Aus mathematischer Sicht sind die Eigenschaften der Zielfunktion, die in der Optimierung betrachtet wird, sehr interessant: Diese sind oft nur stückweise differenzierbar, was aber bei der Differenzenquotienten keine Probleme macht- außer es tritt ein Pol auf. Mit der Berechenbarkeit von Ableitungen stehen sehr effiziente Gradienten-basierte Optimierungsverfahren zur Verfügung, jedoch ist die Zielfunktion nicht ableitbar, so werden die erwünschten Konvergenzeigenschaften eventuell nicht erreicht. Ebenso interessant ist der Bereich der numerischen Integration, da auch hier Schwierigkeiten bei geringer Ableitbarkeit der Integranden auftreten können: Effiziente Verfahren höherer Ordnung werden nur dann schneller zum Ergebnis führen, wenn es stückweise höhere Ableitungen der Funktionen gibt, die auch beschränkt bleiben. Ebenso gibt es die Frage der Schrittweite oder der Diskretisierung in der numerischen Differenziation. Diese Fragestellungen führen auf das Gebiet der numerischen Stabilität: Hier stellt man sich nicht die Frage, ob der Roboter steht, sondern ob überhaupt ein Ergebnis berechenbar oder das Berechnete glaubhaft oder mit mehr Rechenkapazität überhaupt genauer berechnet werden kann. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 16 Jul 2015 | Wilde Singularitäten | 00:26:25 | |||||||||||||||||
Anja Randecker befasst sich in ihrer Forschung mit so genannten wilden Singularitäten, die im Zusammenhang mit Translationsflächen auftreten, und erklärt im Gespräch mit Gudrun Thäter die Faszination dieser mathematischen Konstruktionen. Translationsflächen sind im klassischen Fall Polygone in der Ebene, die an ihren Kanten topologisch verklebt werden. Beim Quadrat erhält man beispielsweise einen Donut, oder auch Torus: (Animation von Kieff zum Verkleben, veröffentlicht als Public Domain): Lokal betrachtet verhält sich eine Translationsfläche wie eine Ebene, da man lokal immer eine Abbildung, eine mathematische Kartenabbildung, von einem kleinen Gebiet der Fläche in ein Gebiet der Ebene angeben kann - dabei geht aber die globale Gestalt der Fläche verloren. Man sieht also nicht mehr, dass der Donut in der Mitte ein Loch hat. Das entspricht dem Problem der Erstellung von Landkarten, was lokal zwar sehr gut funktioniert, aber bei größeren Flächen müssen die Kartenprojektionen starke Verzerrungen in Kauf nehmen. Beim Verkleben der parallelen Kanten von zwei Fünfecken (eins steht auf der Kante, eins auf der Spitze) werden, wie im Beispiel zuvor, alle Ecken miteinander identifiziert und werden zu einem Punkt. Dann erhält man ein Objekt, das wie zwei zusammengebackene Donuts aussieht. Dort verhalten sich alle Punkte auf dem Objekt wie zuvor, bis auf den Punkt, in dem alle Ecken identifiziert sind: Dort hat man einen Panoramablick von 1080 Grad, und somit eine Singularität - genauer eine konische Singularität. Hier hat der Punkt eine Umgebung, die isometrisch zu einer Überlagerung einer Kreisschreibe ist, da wir endliche viele Polygone in der Ebene verklebt haben. Nimmt man hingegen unendliche viele Polygone, oder unterteilt die Kanten in unendlich viele Segmente und verklebt diese, so können die verklebten Ecken eine viel wildere Umgebung haben. Das führt dann zu den so genannten wilden Singularitäten. Diese werden erst seit relativ kurzer Zeit erforscht, sie kommen aber auch bei dynamischen Systemen auf Translationsflächen vor. Hier möchte man in der aktuellen Forschung Begriffe der Konvergenz und damit eine Topologie auf einem Raum der Translationsflächen einführen, um das Verhalten von dynamischen Systemen auf diesem Raum beschreiben und analysieren zu können. Eine Frage ist hier, ob den wilden Singularitäten etwas ähnliches wie die Isometrie zur Kreisscheibe bei den konischen Singularitäten zugeordnet werden kann. Zunächst ist deren Umgebung überraschenderweise wegzusammenhängend. Die Umgebung kann aber auch unendliches Geschlecht besitzen, wie Anja Randecker nun beweisen konnte- die Umgebung hat also unendliche viele Löcher in der Umgebung- und nicht nur ein Loch wie der Donut. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 23 Jul 2015 | Perfekte Gleichgewichte | 00:19:33 | |||||||||||||||||
Wie können wir die globale Erwärmung stoppen? Viola Caspari hat dazu eine spieltheoretische Masterarbeit abgeschlossen. Ihr Interesse galt sogenannten trembling-hand perfekten Gleichgewichten. Dies sind Nash Gleichgewichte mit der besonderen Eigenschaft, dass auch kleine Änderungen in den Daten die Eigenschaft, dass es sich um ein Nash-Gleichgewicht handelt, nicht ändert. Es sind also Strategiekombinationen, die für Entscheidungsfindungen besonders hilfreich sein können. Das Gefangenendilemma ist eines der grundlegenden theoretischen Beispiele aus der Spielttheorie, an dem man verschiedene Strategien illustrieren kann. Als Anwendungsfall behandelte Sie die Verteilung öffentlicher Güter mit unsicherem Schwellwert. Der Hintergrund hierfür sind die laufenden Verhandlungen zwischen allen Staaten, die dazu führen sollen, dass eine mittlere Erwärmung um 2 Grad Kelvin oder mehr vermieden werden kann. Die Erwärmung ist direkt gekoppelt an den CO2-Ausstoß der Staaten. Und natürlich haben alle Staaten Einfluss darauf, wie ihre CO2-Bilanz aussieht. Sie können beispielsweise Geld investieren, um Kohlekraftwerke durch erneuerbare Energieerzeuger abzulösen oder Filter in Schornsteine einbauen, und vieles mehr. Im Modell werden aus den Staaten also Spieler mit verschiedenen Strategien als Handlungsoptionen. Jede Strategie ist mit Kosten verbunden aber auch mit dem Nutzen in Form von eingesparten CO2-Ausstoß. Diese Relationen variieren auch nach der Größe der Wirtschaft der Länder. Gesucht sind nun Handlungsempfehlungen, die dafür sorgen, dass die Staaten solche Absprachen treffen, dass die Schwelle für die katastrophale Klimaveränderung aussbleibt und sich auch an diese Absprachen halten. Eine gute Methode hierfür ist die Einigung auf trembling-hand perfekte Nash-Gleichgewichte, weil hier eine Änderung der eigenen Strategie nur zur Verschlechterung für einen selbst führt. Der Egoismus dient also als Antrieb, sich an getroffene Abmachungen zu halten. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 30 Jul 2015 | Splitting Waves | 00:19:44 | |||||||||||||||||
To separate one single instrument from the acoustic sound of a whole orchestra- just by knowing its exact position- gives a good idea of the concept of wave splitting, the research topic of Marie Kray. Interestingly, an approach for solving this problem was found by the investigation of side-effects of absorbing boundary conditions (ABC) for time-dependent wave problems- the perfectly matched layers are an important example for ABCs. Marie Kray works in the Numerical Analysis group of Prof. Grote in Mathematical Department of the University of Basel. She did her PhD 2012 in the Laboratoire Jacques-Louis Lions in Paris and got her professional education in Strasbourg and Orsay. Since boundaries occur at the surface of volumes, the boundary manifold has one spatial dimension less than the actual regarded physical domain. Therefore, the treatment of normal derivatives as in the Neumann boundary condition needs special care. The implicit Crank-Nicolson method turned out to be a good numerical scheme for integrating the time derivative, and an upwinding scheme solved the discretized hyperbolic problem for the space dimension. An alternative approach to separate the signals from several point sources or scatterers is to apply global integral boundary conditions and to assume a time-harmonic representation. The presented methods have important applications in medical imaging: A wide range of methods work well for single scatterers, but Tumors often tend to spread to several places. This serverely impedes inverse problem reconstruction methods such as the TRAC method, but the separation of waves enhances the use of these methods on problems with several scatterers. Literature and additional material
| |||||||||||||||||||
| 06 Aug 2015 | Sprache PDGL | 00:31:59 | |||||||||||||||||
Catherine Bandle war bis 2003 Professorin am Mathematischen Institut der Universität in Basel. Aber auch über die Emeritierung hinaus ist sie sehr rege in der Forschung zu elliptischen und parabolischen partiellen Differentialgleichungen. Das zeigt sich an einer beeindruckenden Zahl von Publikationen, der Teilnahme an Tagungen und im Einbringen ihrer Erfahrung in die Tätigkeit von Gremien wie dem Landeshochschulrat Brandenburg und dem Steering Committee of the European Science Foundation program: Global and Geometric Aspects of Nonlinear Partial Differential Equations. Ihre Faszination für die Vielseitigkeit dieses Themas in den Anwendungen und die Zusammenhänge zur Geometrie haben sich über viele Jahrzehnte erhalten. Für den Workshop Nonlinear Days 2015 wurde sie für einen Hauptvortrag nach Karlsruhe eingeladen. Wir haben diese Gelegenheit genutzt, das Thema der Modellbildung mit Hilfe von partiellen Differentialgleichungen mit ihr etwas allgemeiner zu beleuchten. Traditionell stehen elliptische wie parabolische Gleichungen am Beginn der modernen Modellbildung von Prozessen in der Physik, der Biologie und Chemie. Hier sind es Diffusions-, Reaktions-, Transport- und Wachstumsprozesse, die zunächst durch gewöhnliche Differentialgleichungen beschrieben wurden. Allerdings waren vor etwa 150 Jahren die Anwendungen in Teilen schon zu komplex für dieses zu einfache Modell. Abhängigkeiten von Veränderungen in allen Raum- und der Zeitrichtung sollten interagierend erfasst werden. Das führte zwingend auf die partiellen Differentialgleichungen. Mit dem Aufstellen der Gleichungen verband sich die Hoffnung, durch die zugehörigen Lösungen Vorhersagen treffen zu können. Um diese Lösungen zu finden, brauchte es aber ganz neue Konzepte. Am Anfang der Entwicklung standen beispielsweise die Fourierreihen, die (unter den richtigen Voraussetzungen) eine Darstellung solcher Lösungen sein können. Werkzeuge wie Fourier- und Lapalacetransformation konnten zumindest für bestimmte Geometrien hilfreiche Antworten geben. Später wurder der Begriff der schwachen Lösung bzw. schwachen Formulierung geprägt und die damit verbundenen Sobolevräume auf verschiedenen Wegen entwickelt und untersucht. Die Suche nach den Lösungen der Gleichungen hat damit die theoretische Entwicklung in der Mathematik stark vorangetrieben. Heute sind wir froh, dass wir in der linearen Theorie (siehe auch Lemma von Lax-Milgram) vieles verstanden haben und versuchen uns Stück für Stück nichtlineare Modellen anzueignen. Ein erster Schritt ist häufig eine lokale Linearisierung oder das Zulassen von Nichtlinearitäten in untergeordneten Termen (semilineare Probleme). Ein integraler Bestandteil ist hier jedoch auch die Möglichkeit, mehr als eine Lösung der Gleichung zu haben und wir brauchen deshalb Konzepte, die physikalisch relevante unter ihnen zu finden. Hier sind Konzepte der Stabilität wichtig. Nur stabile Lösungen sind solche, die zu beobachtbaren Phänomenen führen. Wichtige Werkzeuge in der Lösungstheorie sind auch die Normen, in denen wir unsere Lösungen messen. Am überzeugendsten ist es, wenn sich Normen in Energien des Systems übersetzen lassen. Dann kann man auch die Stabilität im Rahmen von Energieerhaltung und Energieminimierung diskutieren. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 13 Aug 2015 | Photobioreaktoren | 00:35:19 | |||||||||||||||||
Photobioreaktoren sind eine große Hoffnung für unsere Zukunft ohne Erdöl. Sie nutzen die Tatsache aus, dass verschiedenste Algensorten für uns nützliche Stoffe produzieren können. Im einfachsten Fall Futter für unsere Tiere, aber auch Äthanol als Treibstoff oder allgemein als Energieträger. Bei Grünalgen ist die Photosynthese der wichtige Stoffwechselprozess, der natürlich auch Licht braucht und Kohlendioxid. Bevor Photobioreaktoren wirklich effektiv arbeiten können, müssen jedoch viele Aspekte des Prozesses noch viel besser verstanden werden. Hier stehen wir erst am Anfang der Entwicklung. Judith Kolbe hat in ihrer Masterarbeit ein Modell erprobt, das die Verklumpung (technisch: Agglomeration) von Algen beim Fließen durch geschlossene Zylinder beschreiben soll. Das Anliegen ist, durch vorherige Simulation die Bedingungen im Reaktor so zu optimieren, dass die Verklumpung möglichst vermieden wird, damit es nicht zu Fäule und zum Absterben der Algen kommt. Besondere Effekte am Rand des Behälters wurden hier zunächst gar nicht betrachtet. Als Beispielfall wurden sehr kleine Algen- Mikroorganismen- betrachtet, für die die eigene Geometrie keine allzu große Rolle bei der Verklumpung spielt. Der wichtigste Aspekt im Modell ist die Annahme, dass die kugelförmigen Partikel einen Schmierfilm auf ihrer Oberfläche tragen. Zwei Partikel, die während ihrer Bewegung im Fluid zufällig zusammenstloßen, verschmelzen zu einem größeren, wenn die umgesetzte Energie im Schierfilm dissipieren kann. Die Strömung des Trägerfluids geht hier vor allem als Kraftwirkung auf die Algenpartikel ein (inklusive der Bewegungsrichtung). Der Vorteil dieses Modells ist zum einen, dass es so einfach ist, dass es nur wenige Parameter benötigt und zum anderen, dass die Interpretation der Ergebnisse klar ist (im sogenannten Postprocessing). Ein großer Nachteil ist, dass die Zahl der Partikel, die man einzeln so behandeln kann, durch die Rechenstärke schnell sehr stark eingeschränkt wird, selbst wenn ausgenutzt wird, dass man die Rechnungen hervorragend parallelisieren kann. Deshalb wurde in der Arbeit schließlich auch nur ein prototypischer Würfel von 4mm Seitenlänge in der Mitte des zylindrischen Reaktors simuliert. Literatur und weiterführende Informationen
| |||||||||||||||||||
| 24 Sep 2015 | InSAR - SAR-Interferometrie | 00:40:14 | |||||||||||||||||
Im Rahmen des ersten Alumitreffens im neu renovierten Mathematikgebäude gibt uns unser Alumnus Markus Even einen Einblick in seine Arbeit als Mathematiker am Fraunhofer IOSB, dem Fraunhofer-Institut für Optronik, Systemtechnik und Bildauswertung in Ettlingen in der Arbeitsgruppe zur Analyse und Visualisierung von SAR-Bilddaten. Er befasst sich mit der Entwicklung von Algorithmen für die Fernerkundung, genauer gesagt für die Deformationsanalyse mit Hilfe von SAR-Interferometrie (InSAR). Deformation bezieht sich hier auf Bewegungen der Erdkruste oder auf ihr befindlicher Strukturen, z.B. von Bauwerken. Hinter dem Stichwort SAR-Interferometrie verbirgt sich eine Vielfalt von Verfahren der Fernerkundung, die auf Synthetic Aperture Radar, auf Deutsch Radar mit synthetischer Apertur, beruhen, und die die Fähigkeit der Sensorik ein kohärentes Signal zu verarbeiten zur Erzeugung sogenannter Interferogramme nutzen. Für SAR ist es wesentlich, dass der Sensor bewegt wird. Zu diesem Zweck ist er auf einen Satelliten, ein Flugzeug oder auch auf einem auf Schienen laufenden Schlitten montiert. Für die Mehrzahl der Anwendungen wird er entlang einer näherungsweise geradlinigen Bahn bewegt und sendet in festen Zeitabständen elektromagnetische Signale im Mikrowellenbereich aus, deren Returns er, unterteilt in sehr kurze Zeitintervalle, aufzeichnet. Dabei "blickt" er schräg nach unten, um nicht systematisch von zwei verschiedenen Orten der Erdoberfläche rückkehrende Signale zu vermischen. Herauszuheben ist, dass er unabhängig von der Tageszeit- er beleuchtet die Szene selbst- und weitgehend unabhängig von den Wetterverhältnissen- die Atmosphäre verzögert das Signal, ist aber für diese Wellenlängen (ca. 3cm-85cm) bis auf seltene Ausnahmen durchlässig dafür- Aufnahmen machen kann. Dies ist ein Vorzug gegenüber Sensoren, die im optischen oder infraroten Teil des Spektrums arbeiten, und nachts oder bei Bewölkung nicht die gewünschten Informationen liefern können. Neben der Magnitude des rückgestreuten Signals zeichnet der SAR-Sensor auch dessen Phasenverschiebung gegenüber einem Referenzoszillator auf, die die Grundlage für die Interferometrie darstellt und viele Anwendungsmöglichkeiten bietet. Aus dem aufgezeichneten Signal wird das sogenannte fokusierte Bild berechnet. (Mathematisch gesehen handelt es sich bei dieser Aufgabe um ein inverses Problem.) Die Achsen dieses komplexwertigen Bildes entsprechen eine der Position des Satelliten auf seiner Bahn und die andere der Laufzeit des Signals. Der Zahlenwert eines Pixels kann vereinfacht als Mittel der aufgezeichneten Rückstreuung aus dem Volumen angesehen werden, dass durch das jeweilige Paar aus Bahninterval und Laufzeitinterval definiert ist. Dies ist der Kern von SAR: Die Radarkeule erfasst eine größere Fläche auf dem Boden, so dass das aufgezeichnete Signal aus der Überlagerung aller zurückkehrenden Wellen besteht. Diese Überlagerung wird durch die Fokusierung rückgängig gemacht. Dazu benutzt man, dass ein Auflösungselement am Boden zu allen Returns beiträgt, solange es von der Radarkeule erfasst wird und dabei eine bekannte Entfernungskurve durchläuft. Die Magnitude des sich so ergebenden Bildes erinnert bei hochaufgelösten Aufnahmen auf den ersten Blick an eine Schwarzweißphotographie. Betrachtet man sie jedoch genauer, so stellt man schnell Unterschiede fest. Erhabene Objekte kippen zum Sensor, da die höhergelegenen Punkte näher zu ihm liegen. Hohe Werte der Magnitude, also hohe Rückstreuung, sind in der Regel mit günstigen geometrischen Konstellationen verbunden: Eine ebene Fläche muss dazu beispielsweise senkrecht zum einfallenden Signal ausgerichtet sein, was selten der Fall ist. Geht man an die Grenze des aktuell Möglichen und betrachtet ein Bild einer städtischen Umgebung eines luftgetragenen Sensors mit wenigen Zentimetern Auflösung, so scheint es beinahe in punktförmige Streuer zu zerfallen. Diese werden durch dihedrale (Pfosten) und- häufiger- trihedrale Strukturen erzeugt. Trihedrale Strukturen reflektieren das einfallende Signal parallel zur Einfallsrichtung (man kennt das von den an Fahrzeugen verwendeten, Katzenaugen genannten Reflektoren). Sehr niedrige Rückstreuung ist meist darin begründet, dass kein Signal mit der entsprechenden Laufzeit zum Sensor zurückkehrt, sei es weil keine Streuer erreicht werden (Schatten) oder das Signal auf glatten Flächen vom Satelliten weggespiegelt wird. Für Wellenlängen von einigen Zentimetern sind z.B. asphaltierte oder gepflasterte Flächen glatt, bei Windstille ist es auch Wasser. Daneben gibt es auch kompliziertere Streumechanismen, die zu Magnituden mittlerer Höhe führen, etwa Volumenstreuung in Vegetation, Schnee und Sand, verteilte Streuung an Flächen mit vielen kleinen, homogen verteilten Objekten (z.B. Kiesflächen oder andere Flächen mit spärlicher Vegetation) oder einer gewissen Rauigkeit. Außer diesen gibt es noch viele weitere Möglichkeiten, wie Mehrfachreflektionen oder das Zusammenfallen in verschiedenen Höhen positionierter Streuer in einer Entfernungszelle. Die für die SAR-Interferometrie wesentliche Information aber ist die Phase. Sie kann allerdings nur genutzt werden, wenn zwei oder mehr Aufnahmen aus annähernd der gleichen Position vorliegen. Die grundlegende Idee dabei ist die Betrachtung von Doppeldifferenzen der Phase zweier Pixel zweier Aufnahmezeitpunkte. Um sie zu verstehen nehmen wir zunächst an, dass sich in beiden Auflösungszellen je ein dominanter, punktförmiger Streuer befindet, was so gemeint ist, dass die Phase einer Laufzeit entspricht. Da die Subpixelpositionen unbekannt sind und die Größe der Auflösungszelle um Vieles größer als die Wellenlänge ist, ist die Phasendifferenz zweier Pixel eines einzelnen Bildes nicht verwertbar. In der Doppeldifferenz heben sich die unbekannten Subpixelpositionen allerdings heraus. Die Doppeldifferenz ist in dieser idealisierten Situation die Summe dreier Anteile: des Laufzeitunterschiedes auf Grund der verschiedenen Aufnahmegeometrien, des Laufzeitunterschiedes auf Grund einer relativen Positionsänderung der Streuer während der zwischen den Aufnahmen verstrichenen Zeit und des Laufzeitunterschiedes auf Grund der räumlichen und zeitlichen Variation der atmosphärischen Verzögerung. Diese drei Anteile können jeder für sich nützliche Information darstellen. Der Erste wird zur Gewinnung von Höhenmodellen genutzt, der Zweite zur Detektion von Deformationen der Erdoberfläche und der Dritte, obwohl meist als Störterm angesehen, kann bei der Bestimmung der Verteilung von Wasserdampf in der Atmosphäre genutzt werden. Es stellt sich aber die Frage, wie man diese Terme separiert, zumal noch die Mehrdeutigkeit aufgelöst werden muss, die darin liegt, dass die Phase nur bis auf ganzzahlige Vielfache von zwei Pi bekannt ist. Weitere Fragen ergeben sich, da in realen Daten diese Annahmen für viele Pixel nicht erfüllt sind. Stellt man sich beispielsweise eine Auflösungszelle mit mehreren oder vielen kleineren Streuern vor (z.B. mit Geröll), so ändert sich die Phase der überlagerten Returns mit dem Einfallswinkel des Signals. Sie ändert sich auch, wenn manche der Streuer bewegt wurden oder die beiden Aufnahmen nicht ausreichend genau zur Deckung gebracht wurden. Dies führt dazu, dass die Phase sich um einen schlecht quantifizierbaren Betrag ändert. Man spricht dann von Dekorrelation. Eventuell besteht nach Änderung der physischen Gegebenheiten in der Auflösungszelle keine Beziehung mehr zwischen den Phasenwerten eines Pixels. Dies ist etwa der Fall, wenn ein dominanter Streuer hinzu kommt oder nicht mehr anwesend ist, ein Gelände überschwemmt wird oder trocken fällt. Es stellt sich also die Frage, welche Pixel überhaupt Information tragen, bzw. wie ihre Qualität ist und wie sie extrahiert werden kann. Die Geschichte der SAR-Interferometrie begann nach dem Start des ESA-Satelliten ERS 1 im Jahr 1991 mit einfachen differentiellen Interferogrammen. Das berühmteste ist sicher das vom Landers-Erdbeben 1992 in Kalifornien. Zum ersten Mal in der Geschichte der Wissenschaft war es möglich, das Deformationsfeld eines Erdbebens flächig zu messen, wenn auch nur die Komponente in Sichtlinie des Sensors. Statt Werte hunderter in der Region installierter Messstationen stellte das Interferogramm ein Bild des Erdbebens mit Millionen Datenpunkten dar. Diese Fähigkeit, großflächig Deformationen der Erdoberfläche aufzuzeichnen, besitzt nur die SAR-Interferometrie! Allerdings ist zu bemerken, dass dieses Resultat seine Entstehung auch günstigen Umständen verdankt. Landers liegt in der Mojave-Wüste, so dass die Variation der atmosphärischen Verzögerung und die Dekorrelation vernachlässigbar waren. Dank der Verfügbarkeit eines guten Höhenmodells konnte der Anteil des Laufzeitunterschiedes auf Grund der verschiedenen Aufnahmegeometrien eliminiert werden (man spricht dann von einem differentiellen Interferogramm). Ein weiterer Meilenstein war die Shuttle Radar Topography Mission des Space Shuttle Endeavour im Februar 2000, während der die Daten für ein Höhenmodell der gesamten Landmasse zwischen 54 Grad südlicher Breite und 60 Grad nördlicher Breite aufgezeichnet wurden. Für diesen Zweck wurde die Endeavour mit zwei SAR-Antennen ausgestattet, eine am Rumpf, eine an einem 60 Meter langen Ausleger. Dank zeitgleicher Aufnahmen waren die Phasenanteile auf Grund Deformation und atmosphärischer Verzögerung vernachlässigbar. Dekorrelation auf Grund von Änderungen der physischen Gegebenheiten spielt hier auch keine Rolle. Dem Wunsch nach einem weltweiten, dazu deutlich höher aufgelösten Höhenmodell kommt seit 2010 die TanDEM-X-Mission des DLR nach, bei der die beiden SAR-Antennen von zwei Satelliten im Formationsflug getragen werden. Auch in der Algorithmik gab es entscheidende Fortschritte. Einer der fruchtbarsten war die Erfindung von Permanent Scatterer Interferometric SAR (PSInSAR) um das Jahr 2000, das durch die Verwendung einer längeren Zeitreihe von differentiellen Interferogrammen und einiger neuer Ideen das Problem der Separierung der im vorangehenden Abschnitt genannten Terme löste. Der Ausgangspunkt hierfür war die Entdeckung, dass häufig eine größere Anzahl über lange Zeiträume phasenstabile Streuer, die sogenannten Permanent Scatterer (auch Persistent Scatterer oder PS), gefunden werden können, die man sich vereinfacht als Pixel vorstellen darf, deren Auflösungszelle einen dominanten, punktförmigen, über die Zeitreihe unveränderten Streuer enthält. Auf diese wird nun die Auswertung beschränkt, die vereinfacht folgende Schritte durchläuft:
Als Produkt ergeben sich für jeden PS seine Bewegung in Sichtlinie des Sensors und eine Korrektur seiner Höhenlage relativ zum für die Erzeugung der differentiellen Interferogramme verwendeten Höhenmodell. Seither wurden diese Grundideen modifiziert und verfeinert. Vor allem müssen die Berücksichtigung verteilter Streuer (auch Distributed Scatterer oder DS) für die Deformationsanalyse erwähnt werden, was die Informationsdichte vor allem in ariden Gebieten drastisch erhöhen kann, sowie die SAR-Tomographie, die eine Analyse auch dann erlaubt, wenn zwei oder drei vergleichbar starke Streuer in einer Auflösungszelle vorhanden sind (z.B. wenn ein Streuer am Boden, eine Fensterniche und eine Dachstruktur den gleichen Abstand zum Sensor haben). Die SAR-Interferometrie, insbesondere die Deformationsanalyse, verwendet vor allem mathematische Methoden aus den Bereichen Stochastik, Signalverarbeitung, Optimierungstheorie und Numerik. Besondere Herausforderungen ergeben sich daraus, dass die Vielfalt natürlicher Phänomene sich nur bedingt durch einfache statistische Modelle beschreiben lässt und aus dem Umstand, dass die Datensätze in der Regel sehr groß sind (ein Stapel von 30 Aufnahmen mit komplexwertigen 600 Megapixeln ist durchaus typisch). Es treten lineare Gleichungssysteme mit mehreren Zehntausend Unbekannten auf, die robust gelöst sein wollen. Für die Auflösung der Mehrdeutigkeiten verwenden die fortgeschrittensten Algorithmen ganzzahlige Optimierung. Wavelet-basierte Filterverfahren werden genutzt, um die atmosphärische Verzögerung vom Nutzsignal zu trennen. Im Zusammenhang mit der Schätzung der Variation der atmosphärischen Verzögerung werden geostatistische Verfahren wie Kriging eingesetzt. Statistische Tests werden bei der Auswahl der DS, sowie zur Detektion schlechter Pixel eingesetzt. Bei der Prozessierung der DS spielen Schätzer der Kovarianzmatrix eine prominente Rolle. Die SAR-Tomographie nutzt Compressive Sensing und viele weitere Verfahren. Zusammenfassend lässt sich sagen, dass die SAR-Interferometrie auch aus Perspektive eines Mathematikers ein reichhaltiges und spannendes Arbeitsgebiet ist. Eine wichtige Anwendung ist die Deformationsanalyse durch die InSAR-Methode: Die SAR-Interferometrie zeichnet sich vor allen anderen Techniken dadurch aus, dass sie bei geeignetem Gelände sehr großflächige Phänomene mit sehr hoher Informationsdichte abbilden kann. Allerdings liefert sie relative Messungen, so dass in der Regel eine Kombination mit Nivellement oder hochgenauen GPS-Messungen verwendet wird. Ihre Genauigkeit hängt neben der Qualität der Daten von der Wellenlänge ab und zeigt bei 3cm Wellenlänge meist nur wenige Millimeter je Jahr Standardabweichung. Damit können selbst sehr feine Bewegungen, wie z.B. die Hebung des Oberrheingrabens (ca. 2mm/y), nachgewiesen werden. Allerdings können wegen der Mehrdeutigkeit der Phase Bewegungen auch zu stark sein, um noch mit PSInSAR auswertbar zu sein. In diesem Fall können längere Wellenlängen, höhere zeitliche Abtastung oder Korrelationsverfahren helfen. Trotz der diskutierten Einschränkungen lässt sich die Deformationsanalyse mit InSAR in vielen Zusammenhängen nutzensreich einsetzen, denn auch die Ursachen für Deformationen der Erdoberfläche sind vielfältig. Neben geologischen und anderen natürlichen Phänomenen werden sie von Bergbau, Förderung von Wasser, Erdgas, Erdöl, durch Geothermiebohrungen, Tunnelbau oder andere Bautätigkeiten ausgelöst. Meist steht bei den Anwendungen die Einschätzung von Risiken im Fokus. Erdbeben, Vulkanismus, aber auch Schäden an kritischer Infrastruktur, wie Deichen, Staudämmen oder Kernkraftwerken können katastrophale Folgen haben. Ein weiteres wichtiges Thema ist die Entdeckung oder Beobachtung von Erdbewegungen, die sich potentiell zu einem Erdrutsch entwickeln könnten. Allein in den Alpen gibt es tausende Bergflanken, wo sich größere Bereiche in langsamer Bewegung befinden und in Leben oder Infrastruktur gefährdende Hangrutsche münden könnten. Auf Grund der zunehmenden Erderwärmung nimmt diese Bedrohung überall dort zu, wo Permafrost zu tauen beginnt, der bisher den Boden stabilisierte. InSAR wird bei der Erstellung von Risikokarten genutzt, die der Beurteilung der Gefährdungslage und der Entscheidung über Gegenmaßnahmen dienen. In vielen Regionen der Erde werden Deformationen der Erdoberfläche durch veränderte Grundwasserstände verursacht. Nimmt das Grundwasser ab, etwa wegen Entnahme zur Bewässerung oder industriellen Verwendung, so senkt sich die Erdoberfläche. Nimmt das Grundwasser während regenreicher Zeiten zu, so hebt sich die Erdoberfläche. Das Monitoring mit InSAR ist hier aus mehreren Gründen interessant. Bewegungen der Erdoberfläche können Schäden an Gebäuden oder anderen Strukturen verursachen (Bsp. Mexico City). Übermäßige Wasserentnahme kann zu irreversibler Verdichtung der wasserführenden Schichten führen, was Konsequenzen für die zukünftige Verfügbarkeit der lebenswichtigen Flüssigkeit hat. Bei Knappheit muss die Entnahme reguliert und überwacht werden (Bsp. Central Valley, Kalifornien). Von besonderer Bedeutung sind durch geologische Phänomene wie Vulkanismus oder tektonische Bewegungen verursachte Deformationen der Erdoberfläche. Die von SAR-Satelliten gewonnenen Daten werden zur Einschätzung von Risiken benutzt, auch wenn eine sichere, frühzeitige und zeitgenaue Vorhersage von Erdbeben oder Vulkanausbrüchen mit den heutigen Methoden nicht möglich ist. Sie sind aber die Grundlage für eine ausgedehnte Forschungsaktivität, die unser Verständnis der Vorgänge in der Erdkruste stetig wachsen lässt und immer genauere Vorhersagen erlaubt. Dies ist in erster Linie den SAR-Satelliten der ESA (ERS-1, ERS-2, Envisat und aktuell Sentinel-1A) zu verdanken, die seit 1991 mit lediglich einer Lücke von zwei Jahren (2012-2014) kontinuierlich die gesamte Erde aufnehmen. Die Idee dabei ist, dass so in festem zeitlichen Rhythmus (bei ERS alle 35 Tage) jeder Punkt der Erde aufgenommen wird. Dadurch ist ein großes Archiv entstanden, das es nach einem geologischen Ereignis ermöglicht, dieses mit den Methoden der SAR-Interferometrie zu untersuchen, da die Vorgeschichte verfügbar ist. Eine Entwicklung der letzten Jahre ist die Nutzung bei der Erschließung von Erdgas und Erdöl. Die mit InSAR sichtbar gemachten Deformationen erlauben es, neue Einsicht in die Struktur der Lagerstätten zu erhalten, geomechanische Modelle zu kalibrieren und letztlich die Rohstoffe Dank optimierter Positionierung von Bohrlöchern effektiver und kostengünstiger zu fördern. Wer InSAR noch besser verstehen will, der findet in den InSAR Guidlines der ESA die Grundlagen sehr gut erklärt. Einen etwas breiteren Überblick über Anwendungsmöglichkeiten kann man sich auf der Homepage von TRE verschaffen, einem Unternehmen, das von den Schöpfern von PSInSAR gegründet wurde und im Bereich InSAR-Auswertungen nach wie vor führend ist. Die Wettbewerber ADS und e-GEOS bieten außer InSAR weitere Anwendungen von SAR-Daten. Aus wissenschaftlich/politischer Perspektive kann man sich in der Broschüre der DLR über Themenfelder der Erdbeobachtung informieren. Zu dem speziellen Thema der Erdbewegung auf Grund Absenkung des Grundwasserspiegels in den USA gibt es weitere Informationen. Literatur und weiterführende Informationen
| |||||||||||||||||||
| 01 Oct 2015 | Nanophotonics | 00:39:26 | |||||||||||||||||
Nanophotonics is one great path into our future since it renders possible to build e.g. absorber, emitter or amplifier on a scale of a few dozen nanometers. To use this effectively we will have to understand firstly the resonances of plasmons and secondly the interaction of electromagnetic waves with complex media. Here on the one hand we can model light as waves and describe what is happening for the different frequencies of monochromatic light waves. We have to model the evolution in air or in more complex media. On the other hand - taking the more particle centered point of view - we can try to model the reaction of the photons to certain stimuli. The modelling is still in progress and explored in many different ways. The main focus of our guest Claire Scheid who is working on nanophotonics is to solve the corresponding partial differential equations numerically. It is challenging that the nanoscale-photons have to be visible in a discretization for a makro domain. So one needs special ideas to have a geometrical description for changing properties of the material. Even on the fastest available computers it is still the bottleneck to make these computations fast and precise enough. A special property which has to be reflected in the model is the delay in response of a photon to incoming light waves - also depending on the frequency of the light (which is connected to its velocity- also known as dispersion). So an equation for the the evolution of the electron polarization must be added to the standard model (which is the Maxwell system). One can say that the model for the permeability has to take into account the whole history of the process. Mathematically this is done through a convolution operator in the equation. There is also the possibility to explain the same phenomenon in the frequency space as well. In general the work in this field is possible only in good cooperation and interdisciplinary interaction with physicists - which also makes it especially interesting. Since 2009 Claire Scheid works at INRIA méditerranée in Sophia-Antipolis as part of the Nachos-Team and is teaching at the university of Nice as a member of the Laboratoire Dieudonné. She did her studies at the Ecole Normale Superieure in Lyon and later in Paris VI (Université Pierre et Marie Curie). For her PhD she changed to Grenoble and spent two years as Postdoc at the university in Oslo (Norway). Literature and additional material
| |||||||||||||||||||
| 08 Oct 2015 | Klavierstimmung | 00:32:06 | |||||||||||||||||
Wie wirkt sich die Biegesteifigkeit von Klaviersaiten auf die Stimmung aus? Dieser Frage ist Niels Ranosch nachgegangen und erklärt uns im Gespräch mit Gudrun Thäter seine Ergebnisse. Das Schwingen von Klaviersaiten wird oft mit mit der Wellengleichung modelliert und simuliert; die Annahme ist hier, dass die Saite unendlich dünn ist. Betrachtet man die Saite jedoch mit realistischer Querschnittsfläche, so treten durch Dehnung und Stauchung weitere Kräfte im Material auf, und man muss in einem erweiterten Modell gerade für dicke oder kurze Saiten die Biegesteifigkeit der Saiten berücksichtigen. Die Wellengleichung ist eine partielle Differentialgleichung, die die Auslenkung der Saite mit zweiten Ableitungen im Raum und Zeit beschreibt. Zur Erweiterung des Modells wurde die Saite in einzelne Teilfasern aufgeteilt, für die jeweils einzeln die Biegesteifigkeit berücksichtigt wurde. Beim Übergang zu unendliche dünnen Teilfasern erhält man eine erweiterte Differentialgleichung, in der nun auch Raumableitungen vierter Ordnung auftreten. Bei der Lösung des erweiterten Modells ergibt sich nun, dass die Obertöne nicht perfekte Vielfache des Grundtons sind, und daher bei genauer Stimmung des Grundtons nicht harmonisch zu höheren Tönen wären. Daher werden die Grundtöne der Saiten absichtlich leicht verstimmt, damit die Obertöne akzeptabel zu höheren Tönen passen. Ein weiteres Problem für die Harmonie auf dem Klavier liegt im Quintenzirkel oder am Pythagoreischen Komma: Grundsätzlich kann man nicht gleichzeitig Quinten mit Frequenzverhältnis 3/2 und Oktaven mit Frequenzverhältnis 2 auf einem Klavier perfekt stimmen; man kann durch Multiplikation mit 3/2 kein Vielfaches von 2 erreichen. Nach 12 Quinten kommt man dem Ton nach 7 Oktaven sehr nahe, und dies wurde als Grundlage für das Klavier mit 12 Tasten pro Oktave gewählt. Den Fehler versucht man dann mit unterschiedlichen Stimmungen irgendwie erträglich zu machen, wie mit der heutzutage gängigen gleichstufigen Stimmung. Literatur und weiterführende Informationen
| |||||||||||||||||||
| 15 Oct 2015 | Impedanztomographie | 00:30:49 | |||||||||||||||||
Stefanie Hollborn arbeitet an der Universität Mainz am Thema Elektrische Impedanztomographie, die im Vergleich zur Röntgentomographie deutlich weniger schädlich ist und im Vergleich zur Magnetresonanztomographie deutlich preiswerter ist. Mit Hilfe von Elektroden auf der Oberfläche von Objekten wird niedriger Strom auf den Rand des Objektes angelegt und anschließend die resultierende Spannung und dadurch die Impedanz gemessen. Mit Hilfe der daraus abgeleiteten Leitfähigkeitsverteilung im Schnittbild kann man dann Rückschlüsse darauf ziehen, ob im Körper Verunreinigungen vorhanden sind. Dies findet beispielsweise Anwendung bei der Sichtbarmachung, also der Tomographie, von Krebszellen oder beim Auffinden von Blasen in Zement. Der Vorteil des Verfahrens ist, dass es billig einsetzbar und nicht schädlich für lebende Organismen ist. Außerdem sind Kontraste häufig sehr gut auflösbar. Mathematisch werden die Gleichungen für die Wechselwirkung von Strom- und Magnetfeld als Modell zugrunde gelegt. Das Spannungspotential, das als Reaktion auf den Input vom Rand entsteht, lässt sich als Überlagerung von harmonischen Funktionen darstellen. Die Verunreinigungen sind überall da, wo eine harmonische Fortsetzung der Lösung vom Rand her nicht mehr möglich ist. Dort weicht das Feld dann nämlich vom homogenen Verhalten ab, das ohne die Verunreinigung vorliegen müsste. Frau Hollborn arbeitet insbesondere mit Daten die durch ein Paar eng nebeneinander liegende Elektroden entstehen. Die Hoffnung ist, daraus ein einfach einzusetzendes Werkzeug zu machen. Mathematisch muss hier ein eindimensionales Randwertproblem gelöst werden. Die Fortsetzung der Daten ins Innere ist jedoch ein so genanntes schlecht gestelltes Problem, bei dem Fehler verstärkt werden. Dieser Begriff geht zurück auf Jacques Hadamard, der den Begriff der gut gestellten Probleme eingeführt hat. Deshalb benutzt man insbesondere Vorwissen, um die Lösungen zu Regularisieren bzw. die regulären Lösungen aus der Schar aller möglichen Lösungen auszuwählen. Stefanie Hollborn hat sowohl Philosophie als auch Mathematik studiert. Für beide Gebiete ist die Logik ein fundamentales Konzept, wobei die formale mathematische Beschreibung ihre Anwendung sehr erleichtert. Literatur und weiterführende Informationen
| |||||||||||||||||||
| 29 Oct 2015 | Electrodynamics | 00:29:16 | |||||||||||||||||
This episode discusses the Born-Infeld model for Electromagnetodynamics. Here, the standard model are the Maxwell equations coupling the interaction of magnetic and electric field with the help of a system of partial differential equations. This is a well-understood classical system. But in this classical model, one serious drawback is that the action of a point charge (which is represented by a Dirac measure on the right-hand side) leads to an infinite energy in the electric field which physically makes no sense. On the other hand, it should be possible to study the electric field of point charges since this is how the electric field is created. One solution for this challenge is to slightly change the point of view in a way similar to special relativity theory of Einstein. There, instead of taking the momentum ( In the electromagnetic model, the Lagrangian would have to restrict the intensity of the fields. This was the idea which Borne and Infeld published already at the beginning of the last century. For the resulting system it is straightforward to calculate the fields for point charges. But unfortunately it is impossible to add the fields for several point charges (no superposition principle) since the resulting theory (and the PDE) are nonlinear. Physically this expresses, that the point charges do not act independently from each other but it accounts for certain interaction between the charges. Probably this interaction is really only important if charges are near enough to each other and locally it should be only influenced by the charge nearest. But it has not been possible to prove that up to now. The electrostatic case is elliptic but has a singularity at each point charge. So no classical regularity results are directly applicable. On the other hand, there is an interesting interplay with geometry since the PDE occurs as the mean curvature equation of hypersurfaces in the Minkowski space in relativity. The evolution problem is completely open. In the static case we have existence and uniqueness without really looking at the PDEs from the way the system is built. The PDE should provide at least qualitative information on the electric field. So if, e.g., there is a positive charge there could be a maximum of the field (for negative charges a minimum - respectively), and we would expect the field to be smooth outside these singular points. So a Lipschitz regular solution would seem probable. But it is open how to prove this mathematically. A special property is that the model has infinitely many inherent scales, namely all even powers of the gradient of the field. So to understand maybe asymptotic limits in theses scales could be a first interesting step. Denis Bonheure got his mathematical education at the Free University of Brussels and is working there as Professor of Mathematics at the moment. Literature and additional material
| |||||||||||||||||||
| 12 Nov 2015 | RSA-Faktorisierung | 00:20:49 | |||||||||||||||||
Im Rahmen eines Bogy-Praktikums hat Finn Schmidt sich mit dem RSA-Verfahren befasst, einem Vertreter der Asymmetrischen Verschlüsselungsverfahren und eine elementare Basis für private Kommunikation- besonders angesichts der globalen Überwachung, die 2013 nochmal besonders in die öffentliche Aufmerksamkeit rückte. Elementare Rechte, wie das im Grundgesetz gesicherte Recht auf das Postgeheimnis bei einem verschlossenen Briefumschlag, kann man in elektronischen Medien nur durch Kryptoverfahren erreichen. Aus mathematischer Sicht sind Primzahlen grundlegende Bausteine, aus denen RSA-Schlüsselpaare, bestehend aus einem privaten und einem öffentlichen Schlüssel, bestimmt werden. Dazu werden zwei große Primzahlen multipliziert- und das Produkt im öffentlichen Schlüssel preisgegeben. Dies schützt die einzelnen Faktoren, da die Rückrechnung in Form einer Faktorisierung viel aufwendiger als die Multiplikation ist. Zur Betrachtung der Sicherheit des Verfahrens, muss man genau diese Verfahren untersuchen. Ein effizientes Faktorisierungsverfahren ist das Quadratische Sieb, das auf der dritten binomischen Formel basiert. Dazu sucht man zwei Quadratzahlen, deren Differenz die zu faktorisierende Zahl ergibt, da man so eine Faktorisierung erhält. Ein noch besseres Verfahren verspricht der Shor-Algorithmus, jedoch benötigt dieser zur effizienten Ausführung einen Quantencomputer. Das RSA-Verfahren ist bei Betrachtung von Faktorisierungsmethoden auf gängigen Digitalrechnern in dem Sinne sicher, dass die Faktorisierung um Größenordnungen aufwendiger als die Schlüsselerzeugung ist. So kann jedes gewünschte Sicherheitsniveau erreicht werden. Dies ändert sich jedoch sobald Quantencomputer in beliebiger Größe realisiert werden können, da die Faktorisierung mit dem Shor-Algorithmus unmittelbar erfolgen kann. Außerdem werden heute sicher verschlüsselte Texte eventuell mit den leistungsfähigeren Computern der Zukunft in einigen Jahren relativ leicht zu entschlüsseln sein. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 19 Nov 2015 | Brasilien | 00:32:40 | |||||||||||||||||
Ein Auslandsstudium ist eine ganz besondere Ergänzung zum Studium: Benedikt Kottler und Hakan Demirel konnten im Rahmen einer Direktkooperation ihr Studium und ihre Forschungen für ein Semester in Brasilien durchführen. Mit Gudrun Thäter sprechen die beiden über ihre dortigen mathematischen Arbeitsgebiete und ihren Aufenthalt. Benedikt Kottler hat sich in Vorbereitung seiner Master-Arbeit mit der Molekulardynamik befasst. Er möchte die Interaktion von molekularen Partikeln im Rahmen der Kontinuumsmechanik modellieren und mit der Software OpenLB durchführen. Diese Prozesse treten schon in der Betrachtung des Wassermoleküls Das Forschungsthema von Hakan Demirel dreht sich um Feinstaub im Stadtgebiet, genauer um die drei Themen Windsimulation, Partikelsimulation und Feinstaub-Emission durch den Autoverkehr. Dazu konnte er in Brasilien auf eine Verkehrssimulation zurückgreifen und ein stochastisches Modell für Windrichtungen und -intensitäten aufstellen. Dabei hat sich ergeben, dass sich die Stadtgeometrie in der Form von Gebäuden und Straßenzügen einen großen Einfluss auf die sinnvolle Diskretisierung der Windmodelle haben und entsprechend berücksichtigt werden müssen. Die Idee für das Auslandssemester in Brasilien entstand nach einem Vortrag über die Simulationssoftware OpenLB, zu der bestehende Kooperationen zwischen Forschungseinrichtungen in Brasilien und dem KIT bestehen. Die Finanzierung wurde dabei insbesondere durch das Baden-Württemberg-Programm nach Bewerbungsphase ermöglicht. Natürlich gehört auch der Besuch von Vorlesungen zum Auslandsstudium, die teilweise für die beiden in englisch gehalten wurden- und sich teilweise von Vorlesungen in Karlsruhe unterschieden. Die positiven Kontakte zu den Studierenden und Gastfamilien in Brasilien gehören dabei genauso zum Austausch, wie die Erfahrungen unterschiedlicher bürokratischer Systeme. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 26 Nov 2015 | Sonnenkollektoren | 00:24:13 | |||||||||||||||||
Durch Unterstützung von dem Fraunhofer Institut für Solare Energiesysteme ISE konnte sich Edwin Hernandez mit der Optimierung von Sonnenkollektoren befassen. Speziell ging es dabei um Thermische Sonnenkollektoren, bei denen das Sonnenlicht einen flüssigen Wärmeträger erhitzt. Diese Träger können Wasser, Salzlösungen oder Öle mit hohen Wärmekapazitäten sein. Gängige Solarkollektoren verwenden inkompressible Fluide, wie Öle oder Wasser unter hohem Druck, die ihre Phase während der Erwärmung und Abkühlung nicht ändern. Die spannende Frage ist nun, wie sich die Verwendung von kompressiblen Fluiden auswirkt, beispielsweise bei Fluiden, die- wie Wasser- bei Erhitzung gasförming werden. Dies hat Edwin Hernandez simuliert. Die Grundlage für die Simulation ist das lang erprobte PFM (plug flow model) im ColSim - Collector Simulation Environment des ISE für inkompressible Fluide, wo vorausgesetzt wird, dass immer die gleiche Masse ein Rohrstück betritt, wie sie das Stück am anderen Ende verlässt. Diese Massenbilanz für ein Rohrstück wird bei kompressiblen Fluiden verletzt, da die gasförmige Phase ein deutlich höheren Platzbedarf hat. Im Modell wird das Rohr Im Kollektor sinnvollerweise eindimensional angesetzt, da die Länge des Rohrs die Dicke bei weitem überschreitet. Darauf werden die Bilanzgleichungen formuliert. Die enstehenden Gleichungen werden diskretisiert und approximativ gelöst. Die Umsetzung eines erweiterten PFM-Verfahrens (EPFM) und der SIMPLER-Methode erfolgte als neues Modul im ColSim - Collector Simulation Environment Framework. Die neue Methode berücksichtigt ein viel umfangreicheres physikalisches Modell, ist im Gegensatz zu den direkten Lösern des PFM-Verfahrens nun aber auch nur iterativ und damit hier mit mehr Rechenaufwand lösbar. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 03 Dec 2015 | Nullnummer | 01:26:52 | |||||||||||||||||
Die Nullnummer eines Podcasts behandelt die Hintergründe, Themen und Motivation für die Reihe. Dazu ist Nele Heise zu Besuch nach Karlsruhe gekommen, und spricht mit Gudrun Thäter und Sebastian Ritterbusch über Podcasts, Wissenschaftskommunkation und den Modellansatz. Nele Heise, M.A., (@neleheise) ist freie Medienforscherin, Mitglied der Graduate School am Research Center Media and Communication Hamburg und beschäftigt sich in ihrem Promotionsprojekt mit den technischen und sozialen Rahmenbedingungen von Podcasting. Von 2005 bis 2011 studierte sie Kommunikationswissenschaft an der Universität Erfurt und war anschließend bis Sommer 2014 wissenschaftliche Mitarbeiterin in dem DFG-Projekt 'Die (Wieder-)Entdeckung des Publikums' am renommierten Hans-Bredow-Institut für Medienforschung an der Universität Hamburg. Als freie Medienforscherin setzt sie sich in Vorträgen, Gastartikeln, Workshops oder Paneldiskussionen mit Prozessen und Folgen des digitalen Wandels, ethischen Aspekten der Onlinekommunikation oder medialer Teilhabe auseinander. Nele kommt ursprünglich aus der freien Radio-Szene und hat 2003/2004 die Thüringen-Redaktion der Jugendzeitschrift SPIESSER aufgebaut. Im Haus der Fakultät für Mathematik am Karlsruher Institut für Technologie (KIT) befindet sich auch das Nationale Institut für Wissenschaftskommunikation (NaWik) und Nele Heise wurde von Prof. Dr. Annette Lessmöllmann eingeladen, im assozierten Master-Studiengang Wissenschaft - Medien - Kommunikation vorzutragen: In Wissen to Go (Folien) stellte sie die Frage: "Was hat Wissenschaftskommunikation mit Podcasts zu tun?". Sie kam neben der Einführung in Podcasts und aktuellen Themen der Wissenschaftskommunikation zu Formaten, die von Wissenschaffenden selbst getragen werden. Besondere Beispiele waren hier Methodisch inkorrekt, der KonScience Podcast und natürlich auch der BredowCast, der mit von ihr initiiert wurde. Diese Darstellung der Wissenschaft, fernab von Hierarchien, sieht sie als ein Produkt des Digitalen Wandels, das zeigt, welche neuen Rollen und Modelle sich in der Wissenschaftskommunikation etablieren könnten. Der Podcast SciComm – wissen, was läuft von den Studierenden des Studiengangs befasst sich entsprechend offensiv mit den aktuellen Themen der Wissenschaftskommunikation und dem Bild der Wissenschaft in den Medien: In SciComm Folge 2 im Gespräch mit Dr. Sven Stollfuß geht es um die Nerds in Big Bang Theory oder CSI und das daraus resultierende Bild der Wissenschaft. Für den Modellansatz Podcast war der von der DLR und ESA ins Leben gerufene Raumzeit Podcast ein prägendes Element, in dem die Gespräche komplexe Themen nicht scheuen oder simplifizieren, sondern sie in der erforderlichen Breite spannend erklären und so die Hörerschaft ernst nehmen. Dieser Ansatz scheint sich auch daran zu bestätigen, dass das vergleichsweise komplizierte Thema der L-Funktionen in der Zahlentheorie eine der gefragtesten Folgen des Modellansatz Podcasts ist. Dies steht im erstaunlichen Widerspruch zum Selbstverständnis der Wissenschaft in abstrakteren Themenbereichen, bei denen oft von einem Desinteresse der Öffentlichkeit ausgegangen wird. Viele Gesprächspartnerinnen im Podcast sind am Ende positiv über die Art der Themenbehandlung überrascht, und das liegt sicher auch an den Eigenheiten des besonderen Mediums. Der Podcasts ist laut Tim Pritlove das "mit Abstand persönlichste Medium überhaupt". Der Raum für Fragen, für die Themen selbst statt Klischees, erleichtert die Kommunikation für die Wissenschaffenden ungemein. So werden auch Ideen, Fehlschläge und überraschende Ansätze der Forschenden zu einem faszinierenden und lehrreichen Kommunikationsthema im Gegensatz zu Publikationen oder vereinfachenden Zusammenfassungen, die sich oft nur auf Resultate reduzieren. Gleichzeitig wird den Forschenden auf eine sehr menschliche Art die Möglichkeit geboten, über ihre mathematischen Ideen, die Faszination und Ergebnisse ihrer Arbeit zu sprechen. Dies trifft natürlich auch auf andere Forschungsgebiete zu, wie beispielsweise Daniel Meßner in den Stimmen der Kulturwissenschaft demonstriert. Auch beim BredowCast oder beim Forschergeist werden die Forschenden im Gespräch mit ihren vielfältigen Facetten und Interessen in natürlicher Weise zum Medium dargestellt. Daher waren die Forscherinnen, Absolventen und Lehrenden für den Modellansatz schon von Anfang an ein Schwerpunkt für die Auswahl der Gespräche. So fanden Themen der aktuellen Wissenschaft und faszinierende Abschlussarbeiten ihren Weg in den Podcast. Aber auch in der Lehre kann der Podcast die traditionellen Angebote unterstützen und häufige Fragen aus Sprechstunden im Dialog sehr zielgerichtet adressieren. Hier ist die Interaktion mit dem Podcast ein spannendes Thema, und Frameworks wie Podlove bieten eine umfassende Lösung, wie Publikation und Feedback für Podcasts gelöst werden kann. Ein Podcast aus der Praxis der Forschung und Lehre bietet auch die Chance, einen ausgewogeneren Einblick in die Realität der Wissenschaft zu liefern: So sprechen im Modellansatz neben Professorinnen auch junge Absolventinnen und Schüler. Dies bietet einmal einen größeren Grad an Identifikation und dies passt auch gerade zu den Ergebnissen der ARD/ZDF-Onlinestudie 2015, die eine höhere Podcastnutzung gerade bei jüngeren Personen aufzeigt. Ebenso zeigt der Podcast den selbstverständlichen Querschnitt von Frauen wie Männern in der Wissenschaft. Auch in der allgemeinen Podcastlandschaft werden die Frauenstimmen immer zahlreicher, wie die von Nele Heise initiierte Liste zeigt, die von der Hörsuppe in ein Flattrboard gebracht wurde: Frauenstimmen im Netz - die Podcasterinnen-Liste. Leider haben Podcasts in der deutschsprachigen Wissenschaftskommunikation noch keinen hohen Stellenwert, obwohl das Medium einzigartige Vorteile besitzt, wie Henning Krause im Beitrag Wissenschaft auf die Ohren: Audiopodcasts beschreibt. Hier können kuratierte Angebote wie die Wissenschaftspodcasts-Seite (@wisspod) den Einstieg erleichtern und die Verbreitung der Angebote im Wissenschaftsraum fördern. Das soll natürlich auch alle interessierten in der Wissenschaft motivieren, selbst das Mikro in die Hand zu nehmen und über ihre Berufung zu sprechen - denn wer kann authentischer die eigene Motivation, Ideen und Ergebnisse vermitteln als man selbst? Für den Start gibt es viele Anlaufpunkte, wie das Sendegate, das jährliche Wissenschaftspodcaster Treffen #GanzOhr, die Podlove Podcaster Workshops oder Podcast MeetUps in der Nähe. Die Community bietet viel Unterstützung, und so war Toby Baier beispielsweise eine große Hilfe beim Start des BredowCast. Eine Besonderheit von Podcasts ist auch die Verknüpfung des gesprochenen Worts mit den Sendungsnotizen oder Shownotes. Gerade in der Wissenschaft haben Referenzen einen hohen Stellenwert: Es geht hier um Sichtbarkeit, die Herstellung des Kontexts, die Vernetzung mit weiteren Quellen und die Belege für Aussagen. Dies kann und sollte daher in wissenschaftlichen Podcasts eine besondere Aufmerksamkeit erhalten: Neben der traditionellen Referenzierung können sprachliche Ungenauigkeiten detailliert oder korrigiert werden, und die im erwünscht flüssigen Gespräch schwierigen Querverweise nachträglich im Text erfolgen. Letztlich bieten die Texte auf dem Stand der Technik von Suchmaschinen noch eine besonders gute Auffindbarkeit der sonst schwer durchsuchbaren Audiodateien. Eine weitere interessante Ergänzung ist die Erstellung von EBooks, wie Helfrich et al. in Visualization of lithosphere subduction: application to the mantle evolution beneath the Japanese Islands demonstrieren. Hier können schriftliche Medien mit Videos und Tonmedien interaktiv zum erlebenden Lernen zusammengeführt werden. Gerade im Bereich der Lehre können Podcasts den Studierenden und den Lehrenden große Vorteile bringen: Neben dem Ansatz im Flipped Classroom das passive Lernen nach Hause und das aktive Lernen in die Vorlesung zu bringen, haben sich schon die Zusammenfassungen von ganzen Vorlesungen sehr bewährt. Im Modellansatz gibt es dazu die Beispiele der Vorlesungen zur Analysis oder die digitalen Währungen. Dabei sind die Folgen aber keine traditionellen Vorlesungsmitschnitte, sondern spannende Gespräche mit Dozent oder Übungsleiter, wo durch die Unterhaltung die Motivation deutlich steigt. Dabei müssen natürlich nicht alle Darstellungen so spektakulär sein wie das Intro der Folge 62 von Methodisch Inkorrekt (mit dem Reinhard Remfort nichts zu tun hatte). Für den Spracherwerb und auch zur Behandlung von Trauma- und Suchtpatientinnen haben sich Audiopodcasts als begleitendes Medium bewährt und es gibt in der Artikelliste von Nele Heise zum Thema Podcasts wissenschaftliche Studien zu diesem Thema. Interessant sind auch Podcast-Konzepte mit einem vordefiniertem Umfang, wie beispielsweise dem Grounded Theory Podcast (Grounded Theory auf Soundcloud). Die Gespräche werden von den Stimmen getragen - seien es so erfahrene Podcasterinnen wie Annik Rubens oder der Wissenschaftler, der zuvor nie in ein Mikro gesprochen hat - sie alle stellen die Vielfalt der Mitwirkenden dar. Gerade im Audiopodcast werden unterschiedliche Stimmen sehr offen aufgenommen und bieten einen viel tieferen persönlichen Bezug zwischen Hörerin und Sprecherin. Der Blick in die USA zeigt, welchen Stellenwert Podcasts in der Gesellschaft haben können, der sich laut Marco Arment auch noch deutlich erweitern wird. Auch die Entwicklung der Wissenschaftskommunikation ist laut dem SciComm Gespräch mit Prof. Scheufele deutlich weiter. Was sich von diesen Entwicklungen in den deutschsprachigen Raum überträgt, wird sicher auch auf die Wissenschaftspodcasts einen großen Einfluss haben. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 10 Dec 2015 | Population Models | 00:22:49 | |||||||||||||||||
How do populations evolve? This question inspired Alberto Saldaña to his PhD thesis on Partial symmetries of solutions to nonlinear elliptic and parabolic problems in bounded radial domains. He considered an extended Lotka-Volterra models which is describing the dynamics of two species such as wolves in a bounded radial domain: For each species, the model contains the diffusion Starting from an initial condition, a distribution of On a bounded domain, the given boundary conditions are an important aspect for the mathematical model: In this setup, a homogeneous Neumann boundary condition can represent a fence, which no-one, or no wolve, can cross, wereas a homogeneous Dirichlet boundary condition assumes a lethal boundary, such as an electric fence or cliff, which sets the density of living, or surviving, individuals touching the boundary to zero. The initial conditions, that is the distribution of the wolf species, were quite general but assumed to be nearly reflectional symmetric. The analytical treatment of the system was less tedious in the case of Neumann boundary conditions due to reflection symmetry at the boundary, similar to the method of image charges in electrostatics. The case of Dirichlet boundary conditions needed more analytical results, such as the Serrin's boundary point lemma. It turned out, that asymtotically in both cases the two species will separate into two symmetric functions. Here, Saldaña introduced a new aspect to this problem: He let the birth rate, saturation rate and agressiveness rate vary in time. This time-dependence modelled seasons, such as wolves behaviour depends on food availability. The Lotka-Volterra model can also be adapted to a predator-prey setting or a cooperative setting, where the two species live symbiotically. In the latter case, there also is an asymptotical solution, in which the two species do not separate- they stay together. Alberto Saldaña startet his academic career in Mexico where he found his love for mathematical analysis. He then did his Ph.D. in Frankfurt, and now he is a Post-Doc in the Mathematical Department at the University of Brussels. Literature and additional material
| |||||||||||||||||||
| 17 Dec 2015 | Transparent Boundaries | 00:26:17 | |||||||||||||||||
If we are interested in the propagation of waves around a small region of interest, like e.g. an obstacle inside a very big ("unbounded") domain, one way to bring such problems to the computer and solve them numerically is to cut that unbounded domain to a bounded domain. But to have a well-posed problem we have to prescribe boundary conditions on the so-called artificial boundary, which are not inherent in our original problem. This is a classical problem which is not only connected to wave phenomena. Sonia Fliss is interested in so-called transparent boundary conditions. These are the boundary conditions on the artificial boundaries with just the right properties. There are several classical methods like perfectly matched layers (PML) around the region of interest. They are built to absorb incoming waves (complex stretching of space variable). But unfortunately this does not work for non-homogeneous media. Traditionally, also boundary integral equations were used to construct transparent boundary conditions. But in general, this is not possible for anisotropic media (or heterogenous media, e.g. having periodic properties). The main idea in the work of Sonia Fliss is quite simple: She surrounds the region of interest with half spaces (three or more). Then, the solutions in each of these half spaces are determined by Fourier transform (or Floquet waves for periodic media, respectively). The difficulty is that in the overlap of the different half spaces the representations of the solutions have to coincide. Sonia Fliss proposes a method which ensures that this is true (eventually under certain compatibility conditions). The chosen number of half spaces does not change the method very much. The idea is charmingly simple, but the proof that these solutions exist and have the right properties is more involved. She is still working on making the proofs more easy to understand and apply. It is a fun fact, that complex media were the starting point for the idea, and only afterwards it became clear that it also works perfectly well for homogeneous (i.e. much less complex) media. One might consider this to be very theoretical result, but they lead to numerical simulations which match our expectations and are quite impressive and impossible without knowing the right transparent boundary conditions. Sonia Fliss is still very fascinated by the many open theoretical questions. At the moment she is working at Ecole Nationale Supérieure des Techniques avancées (ENSTA) near Paris as Maitre de conférence. Literature and additional material
| |||||||||||||||||||
| 24 Dec 2015 | Qwirkle Gruppe | 01:36:35 | |||||||||||||||||
In vielen Spielen steckt Mathematik, seien es Minecraft, Wasserraketen oder Tiptoi. Lisa Mirlina und Felix Dehnen haben sich Qwirkle (ein Spiel der Schmidt Spiele von Susan McKinley Ross) einmal ganz genau angesehen. Die beiden konnten als Teilnehmer des Hector-Seminar an einem Kooperationsprojekt mit der Fakultät für Mathematik am Karlsruher Institut für Technologie (KIT) teilnehmen. Hier betreute sie Prof. Dr. Frank Herrlich in dem Projekt auf der Suche nach der perfekten Qwirkle-Lösung- wofür die beiden ihm ganz herzlich danken. Das Legespiel war 2011 Spiel des Jahres und besteht aus 108 Spielsteinen aus sechs verschiedenen Farben und sechs verschiedenen Formen- jede Kombination kommt dabei dreimal vor. Jeder Spielteilnehmer versucht aus seinen eigenen sechs nachzuziehenden Spielsteinen gleiche Formen oder gleiche Farben auf dem Tisch in Reihen zusammenzulegen. Wie bei Scrabble gibt es für jedes Anlegen Punkte- es müssen aber alle entstehende Reihen korrekt sein- von Farbe oder Form, wie bei Mau-Mau oder Domino. Das Spielziel ist eine möglichst hohe Anzahl von Punkten zu erreichen. Den mathematischen Hintergrund zum Spiel fanden die beiden in der Topologie: Auf einem Tisch kann man höchstens 36 Steine perfekt anordnen- auf einer anderen topologischen Struktur eventuell mehr.
Mit Hilfe von Verklebungen kann man zu Flächen wie beispielsweise auf einem Torus gelangen- wenn man die jeweils die gegenüberliegenden Seiten miteinander verklebt:
Auf einem Torus haben wirklich alle Steine vier Nachbarn- und nicht nur die Steine im Inneren. Die Frage ist nun, ob es möglich ist, eine Fläche zu finden, wo jeder der 108 Steine in genau zwei perfekten Qwirkle-Reihen- also jeder Form oder Farbe- liegen kann. Neben einem Torus kann man durch Verkleben aus einem Quadrat oder Rechteck auch die Sphäre, das Möbiusband, die Projektive Ebene oder die Kleinsche Flasche erzeugen. Dabei sind das Möbiusband, die projektive Ebene und die Kleinsche Flasche nicht mehr orientierbar, da man keinen Normalenvektor angeben kann. Die projektive Fläche hat in ihrer Darstellung durch homogene Koordinaten eine wichtige Anwendung in der Computergrafik, da Verschiebungen auch als lineare Abbildungen umgesetzt werden können und die gesamte Berechnung deutlich erleichtert. Auch frühere Folgen zu Teichmüllerkurven (Modell042) und wilden Singularitäten (Modell060) haben im Modellansatz Podcast Topologie und Verklebungen behandelt. Die Topologie ist dabei überhaupt nicht so theoretisch, wie sie zunächst erscheint- denn da wir nicht auf einer Ebene oder flachen Erde leben, können wir einmal um die Erde herumgehen, und nach langem Weg wieder an dem gleichen Ort wieder ankommen. Wir können auch andere Winkelsummen von Dreiecken bestimmen. Diese Experimente können wir beim Universum leider nicht leicht durchführen, und so ist die Forschung nach der Topologie des Universums sehr aktuell. In der Topologie können Flächen bzw. zwei topologische Räume als äquivalent angesehen werden, wenn sie durch eine Homöomorphie, also durch eine stetige und stetig umkehrbare Abbildung in einander überführt werden können. So ist eine Tasse (mit einem Henkel) zu einem Torus homöomorph- nicht jedoch zu einem Becher ohne Henkel.
Dies führt auf das interessante Gebiet der topologischen Klassifikation der Flächen, denn man kann durch eine genügend feine Unterteilung der Fläche in beispielsweise Dreiecke, einer Triangulierung, zusammen mit einigen Regeln die Art der Fläche bestimmen. Dies führt auf den verallgemeinerten Satz von Euler für orientierbare Flächen, wo Das Drei Häuser-Problem ist ein Knobelrätsel zu diesem Satz, da das Problem auf einer Ebene oder eine Sphäre nicht lösbar ist, jedoch auf dem Torus eine Lösung besitzt.
Für das Qwirkle-Spiel liefert der Dreifach-Torus (oder eine Brezel) eine Lösung für 8 Steine, wo jeweils zwei Steine doppelt sind und daher auf einem Tisch nicht so anzuordnen wären:
Für 18 Steine haben sie eine unsymmetrische Lösung gefunden, die sich nicht so leicht auf mehr Steine erweitern ließ:
Mit der Treppenstruktur wie bei 8 Steinen mit einer 9er Struktur kann man aber eine Lösung aus 108 Steinen konstruieren:
Nach dem Satz von Euler ist diese Lösung auf einer Fläche, die einem Fünf-Torus entspricht- oder einer Brezel mit zwei Löchern zu viel. Dies ist aber nicht die einzige Lösung für 108 Steine- mit Gruppentheorie kann man nach weiteren Lösungen suchen: Denn so, wie die Steine sich nach Verklebung in einer Richtung wiederholen, so können auch Gruppen genau diese Wiederholungen darstellen. Ein sehr einfaches Beispiel ist die zyklische Gruppe aus drei Elementen 0, 1, 2, die man mit der Addition verknüpft, und bei Ergebnissen über 2 wieder drei abzieht, wie man in dieser Verknüpfungstafel ablesen kann:
Auf drei Elementen kann man aber auch die Symmetrische oder Permutations-Gruppe
Durch das direkte Produkt
Aus dieser Gruppe kann man nun wieder eine Fläche erzeugen, die das perfekte Qwirkle-Spiel mit 108 Steinen mit vollkommen symmetrischen Aufbau ermöglicht:
Die Fläche dieser Lösung hat das Geschlecht 37, ist also äquivalent zu einer Tasse mit 37 Henkeln. Mit diesem Projekt starteten Lisa Mirlina und Felix Dehnen bei Jugend forscht- zunächst beim Regionalentscheid, dann beim Landesentscheid und schließlich dem Bundeswettbewerb. Sie gewannen den Preis der Deutschen Mathematiker-Vereinigung (DMV) für besonders kreativen Einsatz der Mathematik. Und dann ging es als Delegation nach Japan. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 14 Jan 2016 | Automorphe Formen | 00:21:30 | |||||||||||||||||
Hans-Georg Rück ist Professor an der Universität in Kassel in der Arbeitsgruppe Algorithmische Algebra und diskrete Mathematik. Im Rahmen des diesjährigen Weihnachtsworkshops der Arbeitsgruppe Zahlentheorie und Algebraische Geometrie an unserer Fakultät sprach er zu Drinfeld automorphen Formen. In unserem Gespräch gehen wir der Frage nach, was das ist und zu welchen strukturellen Einsichten diese Werkzeuge dienen können. Automorphe Form ist ein sehr alter Begriff. Ausgangspunkt sind holomorphe Funktionen z.B. auf der oberen komplexen Halbebene. Statt Funktionen in einer komplexen Variablen werden jedoch Gruppen angewendet. Die automorphen Formen zeichnen sich dadurch aus, dass sie Invarianzeigenschaften unter bestimmten Gruppen haben. Ein einfaches Beispiel für so eine Invarianzeigenschaft ist, wenn eine Funktion z.B. den gleichen Wert für die komplexen Zahlenwerte z und z+1 hat - also periodisch ist. Ein Beispiel für eine komplexere Operation ist es, die Zahl z nicht in eine Funktion einzusetzen, sondern eine Matrix auf sie anzuwenden. Historisch entstanden sind solche Fragestellungen z.B. dadurch, dass man den Umfang von Ellipsen ausrechnen wollte. Gelöst wurde diese Frage mit Hilfe der Weistraßschen ℘-Funktion. Diese erfüllt eine algebraische Gleichung - die sogenannte elliptische Funktion. Hiervon werden ganze Klassen von Funktionen abgeleitet. Insbesondere auch die automorphen Funktionen. Interessant daran ist, dass man gut mit automorphen Funktionen rechnen kann. Die automorphen Formen haben die angenehme Eigenschaft, dass Reihendarstellungen häufig nach einer endlichen Zahl von Gliedern abbrechen und auch Integrale sich durch solche endliche Reihen darstellen lassen. Außerdem hängen sie mit elliptischen Kurven zusammen, die letztlich ein wesentlicher Zugang waren, um den Satz von Fermat zu beweisen. Im Kontext der hier betrachteten Drinfeld automorphen Formen werden statt ganzer Zahlen als Argumente Funktionenkörper als Werte eingesetzt. Ein einfacher Funktionenkörper ist die Menge der Polynome in x. Er lässt sich (so wie der Körper der ganzen Zahlen auf rationale Zahlen erweitert wird) auf rationale Funktionen erweitern. Das Rechnen mit meromorphen Funktionen und Potenzreihen kann man auf Polynome übertragen. Geometrische Interpretationen sind recht einfach. Für die Gruppe GL(2) ist das Grundgebilde eine unterteilte Gerade also ein endlicher Graph. Da es in der Regel Funktionen auf endlichen Gebilden sind, kann man es gut mit Hilfe eines Computer ausrechnen. Die nächsten Schritte in der Untersuchung der Drinfeld automorphen Formen müssen nun sein: Die L-Reihe bestimmen und Werte an kritischen Stellen bestimmen. Hier besteht ein einger Zusammenhang zur Riemannschen zeta-Funktion. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 21 Jan 2016 | Incredible Proof Machine | 02:57:07 | |||||||||||||||||
In den Räumen des Entropia e.V. traf sich Joachim Breitner mit Sebastian Ritterbusch, um ihm von Computerbeweisen und der Incredible Proof Machine (http://incredible.pm/) zu erzählen. Diese hatte er mit Unterstützung von Kollegen und Freunden für einen dreitägigen Workshop im Oktober 2015 am Science College Jülich mit Schülerinnen und Schülern im Start-Stipendium für motivierte und neu zugewanderte Jugendliche in Mittel- und Oberstufe unter Unterstützung der Deutsche Telekom Stiftung entworfen. Der mathematische Beweis ist grundlegender Bestandteil der Mathematik und die Technik des Beweisen wird im Mathematik- oder Informatikstudium vielfach geübt, wie es auch im Modell036 Podcast zur Analysis beschrieben wurde. Dennoch wird das wichtige Thema nur selten in der Schule angesprochen, da korrekte Beweise sehr formal und abstrakt sind. Mit einem spielerischen Zugang wird der Einstieg in die exakte Beweistheorie für Schüler und Mathematik-Interessierte nicht nur möglich, sondern ermöglicht auch neue Formen der Lehre wie den Modell051 Flipped Classroom. Beweise gehen von bestehenden Aussagen und festgelegten Axiomen aus, um neue Aussagen oder Erkenntnisse zu belegen. Von der Aussage "es regnet" kann man beispielsweise mit einem fiktiven Axiom "wenn es regnet, werden Straßen nass" schließen, dass gilt: "die Straße ist nass". Und man kann daraus mit der Technik des Widerspruch-Beweis zeigen, dass aus der Aussage "die Straße ist trocken" folgt, dass "es regnet nicht" gilt. Denn (und das ist der Beweis), würde es regnen, so wäre die Straße nass, also nicht trocken. Wann ist aber nun ein Beweis richtig? Diese Frage kann sich jeder selbst beantworten, in dem man einen vorliegenden Beweis versucht nachzuvollziehen. Eine Alternative ist die Beweisprüfung mit dem Computer, wie beispielsweise mit Isabelle. Diese Art von Software richtet sich allerdings in erster Linie an fortgeschrittene Nutzer und setzt Kentnisse in sowohl in der Logik als auch in der (funktionalen) Programmierung voraus, und so suchte Joachim nach einer einfachereren Methode, beweisen zu lernen und die Ergebnisse maschinell zu prüfen. Mit der von ihm kreierten Incredible Proof Machine werden Beweise durch Ziehen und Setzen bildlich erstellt, in der Form eines Graphen. So wird das Beweisen zu einem Puzzle-Spiel mit Erfolgserlebnis, das man nach und nach lösen kann, ohne dabei die exakte Mathematik zu verlassen. In dem Spiel gibt es viele Aufgaben, die zu lösen sind. In der Übersicht sind diese in Lektionen geordnet und zeigen jeweils durch einen breiten Strich, dem Inferenzstrich getrennt, von welchen Aussagen oben man welche Aussagen unten beweisen soll. Wählt man eine Aufgabe aus, so sieht man die gegebenen Aussagen, die oberhalb des Striches waren, als Quellen auf einem Arbeitsblatt. Die zu beweisenden Aussagen erscheinen als Senken. Von den Quellen kann man nun per Maus Verbindungen zu den Senken ziehen- entweder direkt, oder mit Hilfe zusätzlicher Blöcke, bzw. gegebener Beweisregeln, aus einer Toolbox links, die ebenfalls zur Verfügung stehen und weitere gegebene Axiome darstellen. Sind alle offenen Senken bewiesen, so leuchtet unten eine Zeile grün auf, als Bestätigung für einen geschafften Level- eine positive Bestärkung, die nicht ganz so spektakulär ist, wie bei Populous.
Während man auf dem Arbeitsblatt spielt, gibt die Incredible Proof Machine unmittelbar Rückmeldung, falls eine Verbindung so keinen Sinn macht: Will man die Aussage B mit Aussage A beweisen, so wird die Linie zwischen den beiden sofort rot, und gibt dem Spielenden die Hilfestellung, wo mindestens ein Fehler steckt.
Die logischen Aussagen und die gegebenen Beweisregeln verwenden eine gängige Notation zur Beschreibung logischer Verknüpfungen. Ein ∨ (sieht wie der kleine Buchstabe v aus), steht für die logische Oder-Verknüpfung und die Notation stammt vom lateinischen Wort vel. Das umgekehrte Symbol ∧ steht für die logische Und-Verknüpfung. In der ersten Lektion gibt es zwei Blöcke bzw. Beweisregeln für die Und-Verknüpfung: Einmal ein Block mit zwei Eingängen X und Y und einem Ausgang X∧Y, sowie einem Block mit einem Eingang X∧Y und zwei Ausgängen X und Y. Die Lektion 1 behandelt damit den grundlegenden Umgang mit dem System und die Konjugation.
Die Lektion 2 führt die Implikation ein. Eine Implikation, oder auch Folge, beschreibt die Aussage, dass aus einer Aussage eine zweite zwingend folgt. Zur Anwendung einer Implikation gibt es in dieser Lektion eine Beweisregel, die eine Implikation anwendet.
Ein weiterer Block ermöglicht eine Implikation zu erzeugen, in dem die Vorbedingung in einem Einschub angenommen bzw. angeboten wird, und man daraus das Zielereignis dann herleiten muss.
Die Prüfung der Beweise in der Incredible Proof Machine erfolgt durch einen Beweisprüfer in Haskell, einer funktionalen Programmiersprache, die auch schon im Modell047 Podcast zum Tiptoi zur Sprache kam. Der Beweisprüfer wurde mit ghcjs nach JavaScript kompiliert und läuft damit komplett im Browser. Über einen Compiler von Haskell zu Redstone wie in dem Modell056 Podcast zu Minecraft ist leider noch nichts bekannt. Ein lehrreicher Zusammenhang ist hier, dass aus logischer Sicht Implikationen vollkommen korrekt sind, wenn die rechte Seite wahr ist – ohne dass ein ursächlicher Zusammenhang bestehen muss. Wenn also jemand nach Einnahme von offensichtlich unwirksamen Mitteln gesund geworden ist, so ist der logische Schluss, dass nach der Einnahme die Person gesund ist, korrekt. Doch darf man daraus keinesfalls schließen, dass die unwirksamen Mittel dafür der Grund gewesen wären. Das ist ein ähnlicher Fehlschluss wie Cum hoc ergo propter hoc – aus Korrelation folgt keine Kausalität. Die Lektion 3 führt die Disjunktion bzw. Oder-Verknüpfung mit drei neuen Beweisregeln-Blöcken ein, zwei zur Erzeugung einer Aussage mit einer Disjunktion, eine zur Zerlegung einer Disjunktion. Interessant ist dabei besonders die Zerlegung der Disjunktion, da sie auf eine Fallunterscheidung führt.
Man kann auch frei weitere Aufgaben innerhalb der Incredible Proof Machine für sich selbst hinzufügen, neue Vorschläge aber auch auf Github einreichen. Die Lektion 4 behandelt die abstrakte falsche Aussage ⊥. Aus dieser kann man alles folgern, ex falso quodlibet, was dann auch in der ersten Aufgabe zu zeigen ist. Eine besondere Notation ist dabei, dass aus einer Aussage falsch folgt, wie A→⊥. Dies bedeutet einfach nur, dass A nicht gilt, also falsch ist – die Negation von A. In Lektion 5 verlassen wir dann die intuitionistische Logik, die von einer konstruktiven Mathematik ausgeht, hinein in die allgemeinere klassische Logik. Hier wird die Beweisregel vom ausgeschlossenen Dritten (tertium non datur) eingeführt. Dabei sind konstruktive Beweise, die also ohne tertium non datur auskommen, leichter automatisiert zu führen. Für die Aussage "Es gibt eine irrationale Zahl, die mit einer irrationalen Zahl potenziert rational ist" gibt es als Beispiel einen nicht-konstruktiven Beweis: Entweder ist Quadratwurzel von 2 mit sich selbst potenziert rational, oder spätestens das Ergebnis potenziert mit der Quadratwurzel von zwei ist rational, denn das ist 2. Es ist nicht klar, welche Basis die Lösung ist, sondern hier nur, dass es eine der beiden ist. Einen Zusammenhang von der konstruktiven Logik zur Programmierung liefert die Theorie der Curry-Howard-Korrespondenz – man kann Programmieren auch als eine Art Beweisen sehen, und daher sind auch ähnliche graphische Darstellungen als Flussdiagramm möglich. In Lektion 6 werden Quantoren und Prädikate eingeführt. Man kann hier beispielsweise zeigen, wann der Existenzquantor und der Allquantor vertauscht werden dürfen:
Die Lektion 7 behandelt zwei weitergehende Beispiele, die auch umgangssprachlich verständlich sind: Die erste Aufgabe behandelt das Bar-Paradox: Hier gilt es zu beweisen, dass es in jeder nicht-leeren Bar immer eine Person gibt, dass wenn sie trinkt, alle in der Bar trinken. Die zweite Aussage lautet: Wenn jeder Mann einen reichen Vater hat, dann gibt es einen reichen Mann mit einem reichen Großvater.
Die klassische Aussagenlogik kann aber auch über andere Kalküle definiert werden: So demonstriert die Incredible Proof Machine die Verwendung des Hilbert-Kalküls und das NAND-Kalküls. Während das Hilbert-Kalkül besonders theoretisch verwendet wird, liefert das NAND-Gatter als einfacher Logikbaustein Anwendungen bis hin zum Volladierer aus NAND-Gattern. Man kann auch jederzeit neue Beweisregeln oder Lemmas definieren, in dem man alle Bausteine logischer Diagramme mit offenen Ein- und Ausgängen mit gedrückter Shift-Taste anwählt und links zu einem neuen Baustein zusammenführt. Das folgende Bild zeigt die Definition des Beweis durch Widerspruch, und die anschließende Verwendung zu Lösung einer Aufgabe in Lektion 5:
Im Gegensatz zur Incredible Proof Machine soll die Software Isabelle nicht vom Nutzer verlangen, alle Beweise selbst zu führen, sondern unterstützt dabei, Beweise auf einem hohen Abstraktionsgrad zu formulieren und zu beweisen. Ein kleines Beispiel für die Nutzung von Isabelle ist der humorvolle Versuch das allgemeine Dreieck zu definieren – und letzlich die eindeutige Existenz zu beweisen.
Eine wichtige Anwendungen für Computerbeweise ist die formale Prüfung und der Beweis von Computersoftware, wie sie beispielsweise durch die Launchbury Semantik möglich wird. Sehr bekannt ist die Nutzung von rechnerunterstützten Beweisen für das Vier-Farben-Problem, das Hermann Minkowski in einer Topologie-Anfängervorlesung vergeblich versuchte nebenbei zu lösen. Der erste Beweis war noch sehr umstritten, da die Korrektheit der verwendeten Software nicht gesichert war. Erst mit einer formalen Prüfung in Coq wurde der Beweis 2005 allgemein akzeptiert. Eine andere gängige Methode ist auch die Verwendung spezialisierter Verifikationsnumerik, um die Existenz von Lösungen zu beweisen, wie dies auch im Modell019 Podcast zum computerunterstützten Beweisen behandelt wird. Auch die dichteste Kugelpackung, bzw. die Keplersche Vermutung, wurde erst 1998 mit Computerhilfe bewiesen, der zunächst ebenso umstritten war. Erst mit dem Projekt Flyspec konnte 2014 die Korrektheit des Beweises formal bewiesen werden. Im Hintergrund der Aufnahme hört man den Freifunk Karlsruhe, der parallel zu unserem Gespräch ein Treffen in den Räumen des Entropia e.V. hatte. Kinder und Jugendliche, die sich für Programmieren interessieren, sollten sich ein CoderDojo, wie das CoderDojo in Karlsruhe, genauer ansehen. Literatur und Zusatzinformationen
Podcasts
| |||||||||||||||||||
| 28 Jan 2016 | Quantenchaos | 00:31:26 | |||||||||||||||||
Diesmal traf sich Gudrun zum Gespräch mit Anke Pohl, die zur Zeit am Max-Planck-Institut für Mathematik in Bonn arbeitet. Das Thema der Unterhaltung ist Mathematisches Quantenchaos. Anke Pohl untersucht nämlich, welchen Zusammenhang die geometrischen und spektralen Eigenschaften Riemannscher Mannigfaltigkeiten haben.
Historisch ist das Interesse an diesen Eigenschaften und ihren Wechselwirkungen bei physikalischen Betrachtungen entstanden, wie z.B. bei den Studien der Schwingungen einer Membran. Im Jahre 1910 vermuteten Lorentz und Sommerfeld, dass der Flächeninhalt einer Membran (die ein Beispiel für eine Riemannsche Mannigfaltigkeit ist) durch die (Ober-)töne dieser Membran (die durch die Eigenwerte eines gewissen Operators bestimmt sind, der die Schwingungen der Membran beschreibt) bestimmt sind. Bereits kurze Zeit später gelang es Hermann Weyl, diese Vermutung mathematisch zu beweisen. Im Laufe der Zeit ist die Untersuchung solcher Zusammenhänge zu einem Teilgebiet der Mathematik und Mathematischen Physik angewachsen, welches sowohl hinsichtlich Motivation als auch in Bezug auf Methoden eng mit diversen anderen Teilgebieten der Mathematik, wie z.B. der Geometrie, der Zahlentheorie und der Analysis, zusammenhängt. Und auch heute noch liefern physikalische Erkenntnisse und Intuitionen gute Heuristiken bzw. sind wegweisend für mathematische Ansätze. Aktuelle große Vermutungen mit sowohl mathematischer als auch physikalischer Motivation sind beispielsweise die Rudnick-Sarnak Vermutung über eindeutige Quantenergodizität auf gewissen kompakten Riemannschen Mannigfaltigkeiten (Gleichverteilung von Eigenfunktionen im Mittel bei wachsendem Eigenwert; für den Beweis von eindeutiger arithmetischer Quantenergodizität wurde E. Lindenstrauss 2010 eine Fieldsmedaille verliehen), die Phillips-Sarnak Vermutung über die (Nicht-)Existenz von quadrat-integrierbaren Eigenfunktionen auf gewissen nicht-arithmetischen Mannigfaltigkeiten, die Sarnaksche Vermutung über das Größenwachstum von Eigenfunktionen bei wachsendem Eigenwert, oder die Sjöstrandsche Vermutung über die asymptotische Anzahl von Resonanzen in Streifen bei hyperbolischen Flächen unendlichen Inhalts. Details und weiterführende Informationen zu diesen und anderen Vermutungen sind beispielsweise in den Übersichtsartikel in den untenstehenden Referenzen enthalten. Anke Pohls befasst sich zur Zeit mit bestimmten Flüssen, den sogenannten geodätischen Flüssen, auf einer speziellen Klasse von Riemannschen Mannigfaltigkeiten. Als erste, recht elementare, Beispiele für Mannigfaltigkeiten kann man sich zunächst Oberflächen vorstellen. Wenn man auf ihnen Größen definiert hat, die zum Messen von Abständen und Winkel dienen, werden sie Riemannsche Mannigfaltigkeit genannt. Wie bei den oben genannten Membranen sind Geodäten. Mathematisch werden die Schwingungen als Lösungen des Laplaceoperators in der zugrundeliegenden Geometrie beschrieben bzw. mit Hilfe der Eigenwerte und Eigenfunktionen des Operators. Aus der Anschauung ist klar, dass die Schwingungen von den geometrischen Eigenschaften der Fläche abhängen. Wenn z.B. die Fläche oder Membran eingerissen ist oder ein Loch hat, klingt sie anders als wenn sie geschlossen ist bzw. gut eingespannt ist. Für kompakte Flächen ist bekannt, dass es unendlich viele solcher Eigenfunktionen gibt. Je nach Grad der Offenheit (also z.B. eine Fläche mit Riss oder Loch) ist es jedoch schwierig zu sagen, wie sich die Schar der Lösungen verändert. Ein interessantes Beispiel wäre z.B. zu betrachten, dass an einer Stelle die eingespannte Fläche im Unendlichen verankert ist, aber das darunterliegende Volumen endlich ist. Vorstellen kann man sich das etwa so, dass man an dieser Stelle die Fläche samt ihren Abständen unendlich weit zieht. Man fragt sich dann, ob eine Welle auf der Fläche auch diese Singularität überlebt. Ein methodischer Ansatz, solche und andere Fragen zu studieren, ist es, Beziehungen zu anderen Objekten, vor allem rein geometrischen, zu finden. Selbergs Beweis zur Unendlichkeit der Anzahl der Eigenfunktionen auf gewissen hyperbolischen Flächen zeigt zunächst, dass die Eigenwerte der Eigenfunktionen (spektrale Objekte) durch die Längen der geschlossenen Geodäten (geometrische Objekte) bestimmt sind. Genauer, sie sind unter den Nullstellen einer generierenden Zetafunktion für das Längenspektrum der Geodäten. Ausnutzung zusätzlicher Eigenschaften der Flächen, wie z.B. Kompaktheit oder zusätzliche Symmetrien, erlaubt dann (manchmal) zu bestimmen, ob Nullstellen existieren und ob sie von Eigenwerten stammen. Anke Pohl schaut sich die Geodäten auf bestimmten hyperbolischen Flächen an, diskretisiert sie und findet ein assoziiertes diskretes dynamisches System auf dem reellen Zahlenstrahl. Für dieses diskrete System sucht sie gewisse invariante Größen, z. B. invariante Maße oder Dichten. Genauer fragt sie nach Eigenfunktionen des assoziierten Transferoperators mit gewissen Parametern (inversen Temperaturen). An dieser Stelle sieht man wieder einen Einfluss aus der Physik: Transferoperatoren entstammen dem thermodynamischen Formalismus der statistischen Mechanik. Sie zeigt dann, dass die Eigenfunktionen dieser Transferoperatoren bijektiv zu den L_2 Eigenfunktionen des Laplaceoperators der hyperbolischen Flächen sind. Da die Eigenfunktionen der Transferoperatoren alleine durch die geschlossenen Geodäten bestimmt sind und somit also geometrische Objekte der Fläche sind, stellt auch sie eine Beziehung zwischen gewissen geometrischen und gewissen spektralen Objekten dieser Flächen her. Zum Abschluss noch eine kurze Erklärung zur Bezeichnung "Quantenchaos" für dieses Themengebiet: Der Laplaceoperator ist gerade, bis auf Skalierung, der Schrödingeroperator in der Physik. Quantenmechanisch werden seine L_2 Eigenfunktionen als gebundene Zustände verstanden. Das zugehörige Objekt in der klassischen Mechanik ist gerade das Hamiltonsche Vektorfeld des geodätischen Flusses, d. h. die Bildungsvorschrift für die Geodäten oder die Bewegungsvorschrift für Kugeln auf der Fläche. Das Korrespondenzprinzip der Physik besagt nun, dass im Grenzfall (hier: Eigenwerte der Eigenfunktionen gehen gegen unendlich) die Gesetze der Quantenmechanik in die der klassischen Mechanik übergehen sollten. Hier fragt man also gerade danach, wie die spektralen und die geometrischen Eigenschaften Riemannscher Mannigfaltigen wechselwirken. Daraus ergibt sich der Bestandteil "Quanten" in "Quantenchaos". Der Bestandteil "Chaos" ist wie folgt motiviert: Bei den in diesem Gebiet studierten Flüssen verhalten sich Bahnen, die sehr nah beieinander starten, typischerweise nach recht kurzer Zeit sehr unterschiedlich. Mit anderen Worten, kleine Änderungen in den Anfangsbedingungen wirken sich typischerweise sehr stark aus, d.h., das System ist in gewisser Weise chaotisch. Frau Pohl hat Mathematik an der TU Clausthal studiert, an der Universität Paderborn promoviert und habilitiert gerade an der Universität Göttingen. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 11 Feb 2016 | Cooking Math | 00:42:56 | |||||||||||||||||
Mathematik mit Kunst und Design erklären- das war ein Ziel des Kurses von Jill Enders und Chris Spatschek im Cooking Math-Projekt über das uns die beiden im Gespräch mit Gudrun Thäter und Sebastian Ritterbusch berichten. Jill und Chris haben an der Hochschule für Gestaltung (HfG) Karlsruhe studiert und mit Science Vision dort ihr Diplom abgeschlossen. Bei Science Vision ging es darum, dass Wissenschaftler und Designer für je eine 10-minütige Präsentation zusammen gebracht wurden, wo die wissenschaftlichen Inhalte ansprechend dargestellt wurden. Das Thema war Jill gut bekannt, da sie das Design der sehr erfolgreichen Science Slams ihrer Schwester Guilia Enders entworfen hatte und schließlich auch die Illustrationen im Bestseller Darm mit Charme erstellte. Im Rahmen des SFB für Wellenphänomene gab es dann die Initiative ein entsprechendes Projekt als Kurs an der HfG für Doktoranden an der Fakultät für Mathematik zu starten. Im Gegensatz zur Science Vision wurde hier die Art der Darstellung offen gelassen. Gestartet hat das Projekt mit Workshops, bei denen die Designergruppen in die mathematischen Inhalte von den Doktoranden eingeführt wurden. Im Anschluss arbeiteten die von Jill und Chris betreuten Teams aus meisst zwei Designern und einem Mathematiker in Kleingruppen selbstständig. Eine erste Vorführung der Ergebnisse gab es beim Sommerloch der HfG und die Schlusspräsentation fand anlässlich des 16. Science Slam in Karlsruhe am 5. November 2015 im Jubez Karlsruhe statt. Eine Ausstellung im Kollegiengebäude Mathematik (und eine weitere Kooperation mit dem SFB) ist für das Jahr 2016 geplant. Literatur und Zusatzinformationen
| |||||||||||||||||||
| 18 Feb 2016 | Splitting | 00:15:37 | |||||||||||||||||
Johannes Eilinghoff befasst sich in seiner Forschung mit mathematischen Fragen in der Quantenmechanik und war mit diesem Thema am Projekt Cooking Math beteiligt. Das Projekt wurde von Promovierenden im Sonderforschungsbereich Wellenphänomene (SFB) an der Fakultät für Mathematik am Karlsruher Institut für Technologie (KIT) und Studierenden der Hochschule für Gestaltung (HfG) unter Federführung von Jill Enders und Chris Spatschek durchgeführt. Kurz vor unserem Gespräch - im November 2015 - waren das Projekt Cooking Math und die entstandenen Arbeiten beim 16. Science Slam Karlsruhe zu Gast, der im jubez stattfand. Die Idee des Projektes ist es, dass Designstudenten von der HfG im Rahmen ihres Studiums die Promotionsprojekte von Mathematikern als Vorlage nehmen, um deren (Teil-)Inhalte kommunizierend zu gestalten. Vorgängerprojekt und zum Teil Anleihe für die Idee war das Projekt Science Vision von Jill Enders und Chris Spatchek. Die Motivation des SFB für die Teilnahme war, die mathematische Forschungsarbeit auf ungewohntem Weg zu kommunizieren. Es waren schließlich sechs Mathematik-Doktoranden und acht Designstudierende an dem Projekt beteiligt. Der Ablauf gestaltete sich wie folgt: An zwei Terminen hielten die Mathematiker Vorträge über ihre Arbeit. Später teilten sich die Designer bestimmte mathematischen Themen (und damit einem der Promovenden) zu und bearbeiteten es in diesen Gruppen weiter. Johannes Eilinghoff hat mit Christina Vinke zusammengearbeitet. Sie hatte die Idee, zunächst einen für ein Laienpublikum verständlichen Text zu schreiben, der die Grundideen der Arbeit von Johannes beinhaltet. Johannes hatte bis dahin schon Erfahrungen mit Vorträgen für mathematisch Vorgebildete, aber hier war es eine besondere Herausforderung den Spagat zwischen der Korrektheit des Textes und seiner Verständlichkeit zu meistern. Die endgültige Version entstand in Zusammenarbeit der beiden (auch mit den beiden Betreuern) und in mehreren Iterationsstufen. Sie wurde im Soundstudio von Johannes eingesprochen und in Abschnitte zu je 2-3 Sätzen unterteilt. Als Visualisiserung des Forschungsgebietes dient außerdem eine auf den Boden gezeichnete Zickzack-Linie, die das Thema von Johannes (Splitting-Verfahren) symbolisiert. Wenn man diese Linie entlangeht, werden jeweils an den Ecken die Teilstrecken die mathematischen Ideen per Kopfhörer vom Band vorgelesen. Johannes schätzt im Rückblick auch den Einblick in die Arbeit an der Hochschule für Gestaltung. Text zum Vorsprechen beim Kunstprojekt „Cooking Math“ mit der Hochschule für Gestaltung. Station 1:
Station 2:
Station 3:
Station 4:
Station 5:
Station 6:
Station 7:
Literatur und Zusatzinformationen
Podcasts
| |||||||||||||||||||
| 25 Feb 2016 | Zeitintegration | 00:30:57 | |||||||||||||||||
Die numerische Zeitintegration gewöhnlicher und partieller Differentialgleichungen ist an der Fakultät für Mathematik ein großes Forschungsgebiet, insbesondere in dem kürzlich gestarteten Sonderforschungsbereich SFB1173 zum Thema Wellenphänomene. Das Ziel dieser Forschung ist es, numerische Verfahren für Probleme zu entwickeln, für die man keine analytische Lösung angeben kann. Patrick Krämer forscht hierbei an besonders effizienten Verfahren für Beispiele aus der Quantenphysik, speziell der Maxwell-Klein-Gordon Gleichung. Darin ist die Klein-Gordon-Gleichung mit den Maxwell-Gleichungen verbunden. Die Klein-Gordon Gleichung ist das relativistische Analogon zur Schrödingergleichung, die die nicht-relativistische Bewegung atomarer Teilchen bzw. dessen Wahrscheinlichkeitsverteilung im Raum modelliert. Durch die Kombination mit den Maxwellgleichungen können nun die Wechselwirkung von elektromagnetischen Feldern mit den Teilchen unter Berücksichtigung relativistischer Effekte beschrieben werden. Die Lösung der Maxwell-Klein-Gordon Gleichung kann als Welle betrachtet werden, die sehr schnelle zeitliche Oszillationen aufweist. Um eine gute numerische Lösung der Maxwell-Klein-Gordon Gleichung zu erhalten, benötigt man Verfahren, die diese Oszillationen gut auflösen können. Für die bisher bekannten Verfahren ist es dafür notwendig sehr kleine Zeitschrittweiten zu wählen. Patrick Krämer verfolgt bei seinem Verfahren nun die Idee, nicht jede einzelne der schnellen Oszillationen zu bestimmen. Stattdessen wird nur die Einhüllende der Welle numerisch berechnet, die sich zeitlich wesentlich langsamer verändert, und anschließend mit der hohen Frequenz der schnellen Oszillation multipliziert. Die Einhüllende lässt sich hierbei numerisch sehr effizient bestimmen, durch Anwendung eines Splitting-Verfahrens auf ein Schrödinger-Poisson System, dessen Lösung nur langsame Oszillationen aufweist und damit deutlich größere Zeitschrittweiten zulässt. Die Arbeit von Patrick Krämer war auch Teil des Cooking Math Projekts, das mit Studierenden der Hochschule für Gestaltung (HfG) unter Federführung von Jill Enders und Chris Spatschek durchgeführt wurde. Die wissenschaftliche Arbeit wurde hier in einen Film umgesetzt, der die Arbeit und Denkweise eines Mathematikers vorstellt. Literatur und Zusatzinformationen
Podcasts
| |||||||||||||||||||
| 03 Mar 2016 | Dynamische Randbedingungen | 00:41:48 | |||||||||||||||||
David Hipp hat am Projekt Cooking Math mitgearbeitet. In seinem darin vorgestellten Forschungsprojekt betrachtet er eine relativ einfache Form der Wellengleichung, die jedoch gut für die Beschreibung von akustischen Wellen geeignet ist. Die Gleichung beschreibt die Wellenausbreitung im Raum mit Hilfe einer partiellen Differentialgleichung. Die Lösung der Wellengleichung ist eine Funktion deren Variablen die Zeit und der Ort sind. Konkret werden in der Gleichung zeitliche und räumliche Änderungen des Zustands, also der Funktion, in Beziehung gesetzt, um die Wellenausbreitung zu beschreiben. Das mathematische Modell für Wellenausbreitung in beschränkten Gebieten umfasst neben der partiellen Differentialgleichung (die hier die Wellengleichung ist) auch noch die Anfangsbedingung, die den Zustand und die Geschwindigkeit zu Beginn des Prozesses festlegt, sowie die Bedingungen am Rand des Gebietes. Physikalisch ist klar, dass Wellen, wenn sie auf die Oberfläche am Rand treffen beispielsweise reflektiert, gebrochen oder gestreut werden können - je nachdem welche Materialeigenschaften der Rand hat. David Hipp untersucht in seiner Forschung insbesondere den Einfluss der Randbedingungen auf die Simulationen solcher Probleme - in seinem Fall also die Wellenausbreitung im Raum. Klassisch wird häufig die Dirichlet oder Neumann-Randbedingung gewählt bzw. die Robin Bedingung als Mischung der beiden. Diese drei Bedingungen auf dem Rand sind allerdings nicht immer realistisch genug, weil sie keine Bewegungen auf dem Rand erlauben.. Deshalb untersucht man derzeit dynamische Randbedingungen - das sind eben solche Bedingungen, die Bewegungen der Welle auf dem Rand zulassen. Damit kann die Wellen Energie an die Wand abgeben und die Wand selbst aktiver Teil der Wellenausbreitung wird. Das kann dann sogar zu Oberflächenwellen auf der Wand führen. Konventionelle numerische Verfahren müssen auf diese neuartigen Randbedingungen erst angepasst werden. Zwar kann David Hipp auf die Finite Elemente Diskretisierung im Raum in Kombination mit klassichen Zeitschrittverfahren zurückgreifen, jedoch muss geprüft werden ob diese Verfahren immer noch so gute Ergebnisse liefern, wie man sie von üblichen Anwendungen gewohnt ist. Eine Herausforderung der dynamischen Randbedingungen ist es, dass unterschiedliche Skalen im Prozess auftreten können, die dann auch so berücksichtigt werden müssen. Zum Beispiel schwingen die Wand und die akustische Welle mit unterschiedlichen Geschwindigkeiten oder Frequenzen. Im Moment genügt es für seine Testrechnungen, das Randgitter der FE-Diskretisierung zu belassen. In Zukunft geht es aber auch darum, hier Anpassungen für unterschiedlichste Materialien möglich zu machen um den verschiedenen Skalen gerecht zu werden. David Hipp ging im Cooking Math Projekt sehr offen und mit wenigen konkreten Vorstellungen in die Zusammenarbeit mit der Hochschule für Gestaltung (HfG) hinein. Schlussendlich ist das vorliegende Ergebnis der Zusammenarbeit mit Oliver Jelko von der HfG eine Mischung aus Lehrvideo zur Mathematik der Wellenausbreitung und professioneller Animation numerischer Testrechnungen für drei unterschiedliche Randbedingungen: Dirichlet, Neumann und akustische Randbedingung. Die akustische Randbedingung ist eine dynamische Randbedingung, die auf der modellhaften Vorstellung beruht, dass die Wand aus vielen winzigen Federn besteht, welche zu schwingen beginnen, wenn sie durch auftreffende akustische Wellen dazu angeregt werden. Als Mathematiker gehört die visuelle Darstellung der Ergebnisse zu unserer Arbeit und ist z.B. auch eine Form von Verifizierung. Aber die professionelle Animation zu Dirichlet-, Neumann und akustischen Randbedingungen durch einen Gestalter ist leichter zugänglich und erlaubt ein intuitives Verständnis. Das Video aus dem Cooking Math Projekt Literatur und Zusatzinformationen
Podcasts
| |||||||||||||||||||
| 10 Mar 2016 | Newton-Verfahren | 00:31:11 | |||||||||||||||||
Mathematik mit Kunst und Design erklären - das war ein Ziel des Cooking Math-Projekts. Robert Winkler forscht an der Fakultät für Mathematik zu numerischen Verfahren für schlecht gestellte Probleme. Das hilft z.B. Elektrische Impedanztomographie genauer und schneller zu machen. Seine Teilnahme am Cooking Math Projektes hat uns zum jetzigen Zeitpunkt zusammengeführt. Die Aufgabenstellung der Elektrischen Impedanztomographie ist es, aus Messungen auf der Oberfläche eines Körpers Rückschlüsse auf die Zusammensetzung im Inneren zu ziehen. Dazu dient bei der Elektrische Impedanztomographie die elektrische Leitfähigkeit im Innern, die Auswirkungen auf gemessene elektrische Potentiale an der Körperoberfläche hat. Aus physikalischen Zusammenhängen (hier Ohmsches Gesetz und Kirchhoffsche Regeln) lassen sich partielle Differentialgleichungen herleiten, die aus der Leitung im Innern die Oberflächenpotentiale berechenbar machen. Das nennt man Vorwärtsproblem. In der Praxis braucht man aber genau die andere Richtung - das sogenannte inverse Problem - denn man hat die Werte auf dem Rand gemessen und will unter den gleichen physikalischen Annahmen auf den Ablauf im Inneren schließen. Der Zusammenhang, der so modellhaft zwischen Leitfähigkeit und Potential am Rand entsteht, ist hochgradig nichtlinear. Außerdem ist er instabil, das heißt kleine Messfehler können dramatische Auswirkungen auf die Bestimmung der Leitfähigkeit haben. Daher müssen bei der numerischen Bearbeitung Verfahren gefunden werden, die die partielle Differentialgleichung numerisch lösen und dabei diese Nichtlinearität stabil behandeln können. Etabliert und sehr effektiv ist dabei das Newtonverfahren. Es ist weithin bekannt zur Nullstellensuche bei Funktionen von einer Variablen. Die grundlegende Idee ist, dass man ausgehend von einem Punkt in der Nähe der Nullstelle den Tangenten an der Funktion folgt um sich schrittweise der Nullstelle zu nähern. Durch die Information, die in der Tangentenrichtung verschlüsselt ist, entsteht so ein Verfahren zweiter Ordnung, was in der Praxis heißt, dass sich nach kurzer Zeit in jedem Schritt die Zahl der gültigen Stellen verdoppelt. Großer Nachteil ist, dass das nur dann funktioniert, wenn man nahe genug an der Nullstelle startet (dh. in der Regel braucht man zuerst ein Verfahren, das schon eine gute erste Schätzung für die Nullstelle liefert). Außerdem gibt es Probleme, wenn die Nullstelle nicht einfach ist. Wenn man das Newtonverfahren zum finden von Optimalstellen nutzt (dort wo die Ableitung eine Nullstelle hat), kann es natürlich nur lokale Minima/Maxima finden und auch nur dasjenige, das am nächsten vom Startwert liegt. Im Kontext der inversen Probleme wird das Newtonverfahren auch eingesetzt. Hier muss natürlich vorher eine geeignete Verallgemeinerung gefunden werden, die so wie die Ableitungen im eindimensionalen Fall eine Linearisierung der Funktion in einer (kleinen) Umgebung des Punktes sind. Der Kontext, in dem das recht gut möglich ist, ist die schwache Formulierung der partiellen Differentialgleichung. Der passende Begriff ist dann die Fréchet-Ableitung. Betrachtet man das Problem mathematisch in einem Raum mit Skalarprodukt (Hilbertraum), kann die Linearisierung mit dem Verfahren der konjugierten Gradienten behandelt werden. Dieses Verfahren findet besonders schnell eine gute Näherung an die gesuchte Lösung, indem es sich Eigenschaften des Skalarprodukts zunutze macht und die aktuelle Näherung schrittweise in besonders "effektive" Richtungen verbessert. Um das lineare Problem stabiler zu machen, nutzt man Regularisierungen und geht von vornherein davon aus, dass man durch Fehler in den Daten und im Modell ohnehin in der Genauigkeit eingeschränkt ist und in der numerischen Lösung nicht versuchen sollte, mehr Genauigkeit vorzutäuschen. Eine typische Regularisierung bei der Elektrische Impedanztomographie ist die Erwartung, dass die Leitfähigkeit stückweise konstant ist, weil jedes Material eine zugehörige Konstante besitzt. Im zugehörigen Cooking Math-Projekt soll der Modellerierungs- und Lösungsfindungsprozess visualisiert werden. Eine Idee hierfür ist das Spiel "Topfschlagen". Literatur und weiterführende Informationen
Podcasts
| |||||||||||||||||||
| 17 Mar 2016 | Helmholtzzerlegung | 00:39:02 | |||||||||||||||||
Jens Babutzka hat Anfang 2016 seine Promotion an der KIT-Fakultät für Mathematik verteidigt. Das Gespräch dreht sich um einen Teil seiner Forschungsarbeit - dem Nachweis der Gültigkeit der sogenannten Helmholtz Zerlegung im Kontext von Gebieten mit einer sich periodisch wiederholenden Geometrie. Das lässt sich für die Untersuchung von photonischen Kristallen ausnutzen unter der Wirkung einer Zeit-harmonischen Wellengleichung. Für die Untersuchung von partiellen Differentialgleichungen auf Lösbarkeit, Eindeutigkeit der Lösungen und deren Regularität gibt es verschiedene Grundwerkzeuge. Eines ist die Helmholtz Zerlegung. Falls sie in einem Raum möglich ist, kann man jedes Vektorfeld des Raumes eindeutig aufteilen in zwei Anteile: einen Gradienten und einen zweiten Teil, der unter der Anwendung der Divergenz das Ergebnis Null hat (man nennt das auch divergenzfrei). Wann immer Objekte miteinander skalar multipliziert werden, von denen eines ein Gradient ist und das andere divergenzfrei, ist das Ergebnis Null. Anders ausgedrückt: sie stehen senkrecht aufeinander. Die Untersuchung der partiellen Differentialgleichung lässt sich dann vereinfachen, indem eine Projektion auf den Teilraum der divergenzfreien Funktionen erfolgt und erst im Anschluss die Gradienten wieder "dazu" genommen, also gesondert behandelt werden. Da die Eigenschaft divergenzfrei auch physikalisch als Quellenfreiheit eine Bedeutung hat und alle Gradienten wirbelfrei sind, ist für verschiedene Anwendungsfälle sowohl mathematisch als auch physikalisch motivierbar, dass die Aufteilung im Rahmen der Helmholtz Zerlegung hilfreich ist. Im Kontext der Strömungsmechanik ist die Bedingung der Divergenzfreiheit gleichbedeutend mit Inkompressibilität des fließenden Materials (dh. Volumina ändern sich nicht beim Einwirken mechanischer Kräfte). Für das Maxwell-System kann es sowohl für das magnetische als auch für das elektrische Feld Divergenzfreiheitsbedingungen geben. Ob die Helmholtz Zerlegung existiert, ist im Prinzip für viele Räume interessant. Grundbausteine für die Behandlung der partiellen Differentialgleichungen im Kontext der Funktionalanalysis sind die Lebesgue-Räume Insbesondere bei der Behandlung von nichtlinearen Problemen reicht es aber häufig nicht, sich auf den Fall Jens Babutzka hat in seiner Promotion unter anderem bewiesen, dass die Helmholtz Zerlegung für Dabei hilft ihm die periodische Struktur der Geometrie. Mithilfe eines erst kürzlich bewiesenen Theorems von Bernhard Barth über Blochoperatoren kann er das Problem auf eine Familie von Phasenoperatoren auf der (beschränkten) periodischen Zelle reduzieren. Falls diese Operatoren regulär genug sind, lassen sie sich fortsetzen von Für beschränkte Gebiete hängt es im Wesentlichen von der Glattheit des Randes ab, ob die Helmholtz Zerlegung in Literatur und weiterführende Informationen
| |||||||||||||||||||
| 24 Mar 2016 | Complex Geometries | 00:32:39 | |||||||||||||||||
Sandra May works at the Seminar for Applied Mathematics at ETH Zurich and visited Karlsruhe for a talk at the CRC Wave phenomena. Her research is in numerical analysis, more specifically in numerical methods for solving PDEs. The focus is on hyperbolic PDEs and systems of conservation laws. She is both interested in theoretical aspects (such as proving stability of a certain method) and practical aspects (such as working on high-performance implementations of algorithms). Sandra May graduated with a PhD in Mathematics from the Courant Institute of Mathematical Sciences (part of New York University) under the supervision of Marsha Berger. She likes to look back on the multicultural working and learning experience there. We talked about the numerical treatment of complex geometries. The main problem is that it is difficult to automatically generate grids for computations on the computer if the shape of the boundary is complex. Examples for such problems are the simulation of airflow around airplanes, trucks or racing cars. Typically, the approach for these flow simulations is to put the object in the middle of the grid. Appropriate far-field boundary conditions take care of the right setting of the finite computational domain on the outer boundary (which is cut from an infinite model). Typically in such simulations one is mainly interested in quantities close to the boundary of the object. Instead of using an unstructured or body-fitted grid, Sandra May is using a Cartesian embedded boundary approach for the grid generation: the object with complex geometry is cut out of a Cartesian background grid, resulting in so called cut cells where the grid intersects the object and Cartesian cells otherwise. This approach is fairly straightforward and fully automatic, even for very complex geometries. The price to pay comes in shape of the cut cells which need special treatment. One particular challenge is that the cut cells can become arbitrarily small since a priori their size is not bounded from below. Trying to eliminate cut cells that are too small leads to additional problems which conflict with the goal of a fully automatic grid generation in 3d, which is why Sandra May keeps these potentially very small cells and develops specific strategies instead. The biggest challenge caused by the small cut cells is the small cell problem: easy to implement (and therefore standard) explicit time stepping schemes are only stable if a CFL condition is satisfied; this condition essentially couples the time step length to the spatial size of the cell. Therefore, for the very small cut cells one would need to choose tiny time steps, which is computationally not feasible. Instead, one would like to choose a time step appropriate for the Cartesian cells and use this same time step on cut cells as well. Sandra May and her co-workers have developed a mixed explicit implicit scheme for this purpose: to guarantee stability on cut cells, an implicit time stepping method is used on cut cells. This idea is similar to the approach of using implicit time stepping schemes for solving stiff systems of ODEs. As implicit methods are computationally more expensive than explicit methods, the implicit scheme is only used where needed (namely on cut cells and their direct neighbors). In the remaining part of the grid (the vast majority of the grid cells), a standard explicit scheme is used. Of course, when using different schemes on different cells, one needs to think about a suitable way of coupling them. The mixed explicit implicit scheme has been developed in the context of Finite Volume methods. The coupling has been designed with the goals of mass conservation and stability and is based on using fluxes to couple the explicit and the implicit scheme. This way, mass conservation is guaranteed by construction (no mass is lost). In terms of stability of the scheme, it can be shown that using a second-order explicit scheme coupled to a first-order implicit scheme by flux bounding results in a TVD stable method. Numerical results for coupling a second-order explicit scheme to a second-order implicit scheme show second-order convergence in the L^1 norm and between first- and second-order convergence in the maximum norm along the surface of the object in two and three dimensions. We also talked about the general issue of handling shocks in numerical simulations properly: in general, solutions to nonlinear hyperbolic systems of conservation laws such as the Euler equations contain shocks and contact discontinuities, which in one dimension express themselves as jumps in the solution. For a second-order finite volume method, typically slopes are reconstructed on each cell. If one reconstructed these slopes using e.g. central difference quotients in one dimension close to shocks, this would result in oscillations and/or unphysical results (like negative density). To avoid this, so called slope limiters are typically used. There are two main ingredients to a good slope limiter (which is applied after an initial polynomial based on interpolation has been generated): first, the algorithm (slope limiter) needs to detect whether the solution in this cell is close to a shock or whether the solution is smooth in the neighborhood of this cell. If the algorithm thinks that the solution is close to a shock, the algorithm reacts and adjusts the reconstruted polynomial appropriately. Otherwise, it sticks with the polynomial based on interpolation. One commonly used way in one dimension to identify whether one is close to a shock or not is to compare the values of a right-sided and a left-sided difference quotient. If they differ too much the solution is (probably) not smooth there. Good reliable limiters are really difficult to find. Literature and additional material
| |||||||||||||||||||
| 31 Mar 2016 | Perkolation | 00:42:13 | |||||||||||||||||
Sebastian Ziesche hat bei Martin Zerner an der Universität in Tübingen Perkolationstheorie kennen gelernt und sich von der Faszination seines akademischen Lehrers anstecken lassen. Er hat nach dem Diplom in Karlsruhe in der Arbeitsgruppe von Günther Last das Vorhaben verfolgt, die Perkolationsmethoden auf zufällige Mosaike zu erweitern und darüber zu promovieren. Dieses Projekt hat er Anfang 2016 erfolgreich abgeschlossen. Perkolation ist ein Modell der statistischen Physik zur Modellierung poröser Strukturen mit Hilfe von Zufallsprozessen. Es geht dabei vor allem um die Quantifizierung von Durchlässigkeit. Als einfachstes Beispiel kann man sich ein regelmäßiges Gitter z.B. in der Ebene oder im Raum vorstellen, in dem jeder Knoten zufällig und unabhängig von allen anderen Knoten mit Wahrscheinlichkeit 1-p entfernt wird. Eine wichtige Frage ist, wie groß Zusammenhangskomponenten in so einer Struktur sein können. Dieses Modell hat nur einen Parameter (mit welcher Wahrscheinlichkeit p verbleibt ein Knoten im Gitter oder nicht) um verschiedene Strukturen unterscheidbar zu machen. Untersuchte Eigenschaften der Zusammenhangskomponeten bzw. Cluster sind Fragen nach deren Durchmesser oder Volumen. In der Regel eignet sich das Zählen von Knoten gut als Entfernungsmaß. Insbesondere die Frage, ob Cluster unendlich groß sein können erweist sich als interessant. Die Wahrscheinlichkeit dafür, dass es unendlich große Cluster gibt, hängt von dem Parameter p ab und ist entweder 0 (unwahrscheinlich) oder 1 (d.h. fast sicher). Das liegt daran, dass nach dem Null-Eins-Gesetz von Kolmogorov Ereignisse, die nicht vom Zustand endlich vieler Knoten abhängen, nur die Wahrscheinlichkeit 0 oder 1 haben können. Nach Überschreiten eines gewissen (sogenannten kritischen) Parameters wird also die Wahrscheinlichkeit, dass es einen unendlich großes Cluster gibt, von 0 auf 1 springen. Das Verhalten im ebenen Fall ist deutlich besser verstanden und zeigt im Dreiecks-Gitter eine gewisse Dualität, da immer entweder die vorhandenen oder die gelöschten Knoten einen unendlich großen Cluster bilden (außer im kritischen Fall). Im drei-dimensionalen Fall hingegen könnten unendlich große Cluster in beiden Mengen gleichzeitig existieren, falls der kritische Parameter kleiner als 1/2 ist. Mathematisch ist das gar nicht so einfach zu untersuchen. Ein typisches Verfahren ist es, Würfel der Kantenlänge n als Repräsentanten in allen möglichst vielen Realisierungen zu simulieren (die uns verfügbare Rechenleistung begrenzt dabei die Anzahl simulierbarer Realisierungen) und aus den so gewonnenen Strukturbeobachtungen auf das unendlich große Gebiet zu schließen. Die Perkolationstheorie fragt anders herum auch nach lokalen Konsequenzen aus dem Wissen um die Existenz unendlich großer Cluster. Die FKG-Ungleichung ist hier in beiden Richtungen (von lokal nach global und umgekehrt) ein Hauptwerkzeug. Sebastian Ziesche hat die Perkolationstheorie, die auf Gittern verstanden ist, auf zufällige Graphen erweitert. In einem zweistufigen Prozess wird also zunächst ein zufälliges Gitter erzeugt, das dann ausgedünnt wird. Ein Beispiel ist ein Voronoi-Mosaik. Die Methoden der klassischen Perkolationstheorie müssen durch Methoden ergänzt werden, die die besonderen geometrische Eigenschaften ausnutzen. In unserem Gespräch unterhielten wir uns außerdem darüber, wie wichtig es ist, dass Wissenschaftler den richtigen Rahmen finden, um junge Leute für ihre Themen zu begeistern und dass die Arbeit am Promotionsprojekt durchaus nicht geradlinig ist sondern von (postiven wie negativen) Überraschungen geprägt ist. Vieles lässt sich zu Beginn nicht absehen. Literatur und weiterführende Informationen
Podcasts
| |||||||||||||||||||
| 07 Apr 2016 | Verkehrswesen | 00:41:03 | |||||||||||||||||
Im Gespräch mit Ulrike Leyn wollten wir den Blick auf Aufgaben im heutigen Verkehrswesen richten. Wir begannen die Unterhaltung damit, zu erkunden, auf welchem Weg Ulrike Leyn zum Verkehrswesen gekommen ist und schließlich für das Thema Feuer gefangen hat. Am Anfang stand wohl ihre Entscheidung für das Studienfach Wirtschaftsingenieurwesen aus dem einfachen und sehr nachvollziehbaren Grund, sich damit thematisch nicht so stark festlegen zu müssen und im Anschluss sehr viele auch sehr verschiedenartige Möglichkeiten des beruflichen Einstiegs zu haben. Im Wirtschaftsingenieurwesen gibt es je nach Universität verschiedene Ausbildungsstrategien. An einigen muss man sich zu Beginn auf eine Ingenieurdisziplin festlegen, die dann mit ökonomischen Fächern kombiniert wird. In Karlsruhe ist die Ausbildung jedoch ingenieurtechnisch sehr breit angelegt. Es werden also Grundlagen für sehr verschiedene Ingenieurwissenschaften im Studium gelehrt und erst in der Vertiefung erfolgt eine Spezialisierung nach eigener Neigung. Außerdem ist auch der Anteil zwischen ökonomisch ausgerichteten und ingenieurstechnischen Fächern am Karlsruher Institut für Technologie (KIT) je nach persönlicher Wahl stark variabel. Das waren zwei Aspekte, die Ulrike Leyn darin bestärkten in Karlsruhe zu studieren. Für sie war es schließlich die Wahl der Fächerkombination 'Grundlagen der Raum- und Infrastrukturplanung', die zum ersten Schritt in die Richtung Verkehrwsesen wurde. Die Interdisziplinarität des Themas hat sie von Anfang an sehr angesprochen. Deshalb schrieb sie schließlich auch ihre Diplomarbeit am Institut für Verkehrswesen. Direkt im Anschluss begann sie, als wissenschaftliche Mitarbeiterin am Institut zu arbeiten. In ihrer jetzigen Tätigkeit im Verkehrswesen kann Ulrike Leyn vor allem ausnutzen, dass sie im Studium gelernt hat, sich in sehr viele verschiedene Probleme selbstständig einzuarbeiten. Außerdem erwies sich ihre Tätigkeit als Tutorin der Vorlesung Programmieren in Java als sehr hilfreich, um Simulationen anzupassen und automatisiert auszuwerten. In Karlsruhe am KIT ist Verkehrswesen als Teil des Bauingenieurwesens an der KIT-Fakultät für Bauingenieur-, Geo- und Umweltwissenschaften etabiliert. Inzwischen gibt es auch einen eigenen Master-Studiengang Mobilität und Infrastruktur. Neben der Möglichkeit als Ingenieurs-Vertiefung im Wirtschaftsingenieurwesen (und der technischen VWL) kann es auch als Zusatzfach in Informatik, Physik oder Wirtschaftsmathematik gewählt werden oder als technisches Fach im Master Technomathematik. Die Lehrangebote des Instituts erstrecken sich über mehrere Bereiche. Das Projekt, an dem Ulrike Leyn für lange Zeit gearbeitet hat und das gerade abgeschlossen wurde, soll die Möglichkeit bieten, Verkehrs-Simulation auf Computern so zu verwenden, dass man sie einfacher als Ergänzung bzw. Ersatz der Richtlinien im Handbuch für die Bemessung von Straßenverkehrsanlagen (HBS) einsetzen kann. Diese Richtlinie hilft die Qualitätsstufe von Anlagen einzuschätzen. Allerdings - insbesondere bei Nicht-Standard-Situationen ist es heute schon üblich, statt der stark vereinfachenden Rechnungen nach dieser Richtlinie, Simulationen zu benutzen. Denn die Voraussetzungen für die Anwendung der Richtlinien sind nur dann gegeben, wenn auch vorher Richtlinen-getreu gebaut wurde für Normalverkehrssituationen. Ein Schwerpunkt der Untersuchungen waren Autobahnen, wo z.B. Ein- und Ausfahrten und starke Anstiege besondere Herausforderungen an die Modellierung stellen. Das Ziel war kurz gesagt das Finden von Parametern, bei denen die durch Simulation erzeugten Ergebnisse denen nach der Richtlinie berechneten entsprechen. Das klingt einfacher als es ist. Ein generelles Problem ist beispielsweise, dass es häufig nicht genug verlässliche Verkehrsdaten gibt bzw. die Güte der Daten nicht offensichtlich ist. Trotzdem soll mit den so gefundenen Einstellungen der Realität möglichst gut entsprechende Simulationen möglich werden - sogar falls keine Daten vorhanden sind - wenn man nun mit den Einstellungen arbeitet, die im Projekt gefunden wurden. Die Parameter sind zugeschnitten auf die Situation auf deutschen Autobahnen (also auch ohne Tempolimit). Der Einfluss verschieden großer Anteile von Schwerverkehr auf der Autobahn wurde untersucht und als etwas vereinfachender Standard dann 10% gewählt. Es gibt neben Standard-LKWs auch längere Zugverbände, die dann mehr Platz brauchen. Das wird auch beim Einfädeln relevant. Bei der Bewertung der Güte der Modelle werden vor allem Endergebnisse von Simulationen für festgelegte makroskopische Größen wie z.B. die Kapazität der Strecke (nämlich typischerweise etwa 2000 PKW-Einheiten pro Fahrstreifen pro Stunde) zugrunde gelegt. Das Messen der Kapazität ist aber gar nicht so einfach, weil man eigentlich nur konkrete Fahrzeuganzahlen pro Zeit- oder Raumeinheit der Simulation oder der Realität entnehmen kann. Die Kapazität ist die Obergrenze für realisierbare Dichten, also das, was kurz vor dem Zusammenbrechen des Verkehrs als maximaler Zustand vorliegt. Eine Verkehrssimulation zum zusammenbrechen zu bringen ist aber nicht so einfach, weil es nicht vorgesehen ist. Verkehrswesen hat viele sehr unterschiedliche Aspekte. Sie reichen von sehr technisch motivierten Arbeitsbildern zu mehr soziologisch geprägten. Letztere sind z.B. Fragen, warum Wege zurückgelegt werden, wie Verkehrsmittel ausgewählt werden und Veränderungen hierbei. Außerdem sind u.a. autonomes Fahren und Elektromobilität neue und spannende Themen. Literatur und weiterführende Informationen
Podcasts
| |||||||||||||||||||
| 14 Apr 2016 | Crop Growth | 00:20:47 | |||||||||||||||||
This is the first of four conversation Gudrun had during the British Applied Mathematics Colloquium which took place 5th – 8th of April 2016 in Oxford. Josie Dodd finished her Master's in Mathematical and Numerical Modelling of the Atmosphere and Oceans at the University of Reading. In her PhD project she is working in the Mathematical Biology Group inside the Department of Mathematics and Statistics in Reading. In this group she develops models that describe plant and canopy growth of the Bambara Groundnut - especially the plant interaction when grown as part of a crop. The project is interdisciplinary and interaction with biologists is encouraged by the funding entity. Why is this project so interesting? In general, the experimental effort to understand crop growth is very costly and takes a lot of time. So it is a great benefit to have cheaper and faster computer experiments. The project studies the Bambara Groundnut since it is a candidate for adding to our food supply in the future. It is an remarkably robust crop, draught tolerant and nitrogent inriching, which means the production of yield does not depend on fertilizer. The typical plant grows 150 days per year. The study will find results for which verfication and paramater estimations from actual green house data is available. On the other hand, all experience on the modelling side will be transferable to other plants up to a certain degree. The construction of the mathematical model includes finding equations which are simple enough but cover the main processes as well as numerical schemes which solve them effectively. At the moment, temperature and solar radiation are the main input to the model. In the future, it should include rain as well. Another important parameter is the placement of the plants - especially in asking for arrangements which maximize the yield. Analyzing the available data from the experimental partners leads to three nonlinear ODEs for each plant. Also, the leave production has a Gaussian distribution relationship with time and temperature. The results then enter the biomass equation. The growth process of the plant is characterized by a change of the rate of change over time. This is a property of the plant that leads to nonlinearity in the equations. Nevertheless, the model has to stay as simple as possible, while firstly, bridging the gap to complicated and more precise models, and secondly, staying interpretable to make people able to use it and understand its behaviour as non-mathematicians. This is the main group for which the models should be a useful tool. So far, the model for interaction with neighbouring plants is the computational more costly part, where - of course - geometric consideration of overlapping have to enter the model. Though it does not yet consider many plants (since green house sized experimental data are available) the model scales well to a big number of plants due to its inherent symmetries. Since at the moment the optimizaition of the arrangements of plants has a priority - a lot of standardization and simplifying assumptions are applied. So for the future more parameters such as the input of water should be included, and it would be nice to have more scales. Such additional scales would be to include the roots system or other biological processes inside the plant. Of course, the green house is well controlled and available field data are less precise due to the difficulty of measurements in the field. During her work on the project and as a tutor Josie Dodd found out that she really likes to do computer programming. Since it is so applicable to many things theses skills open a lot of doors. Therefore, she would encourage everybody to give it a try. Literature and additional material
| |||||||||||||||||||
| 21 Apr 2016 | Fußgängermodelle | 01:01:05 | |||||||||||||||||
Dr. Tobias Kretz arbeitet in der Firma PTV Group in Karlsruhe an der Modellierung und Simulation von Fußgängerströmen. Er studierte Physik an der Universität Karlsruhe und behandelte in seiner Diplomarbeit Teilchen-Zerfallsprozesse. Anschließend führte ihn die Suche nach interessanten Anwendungen physikalischer Konzepte zur Arbeitsgruppe Physik von Transport und Verkehr an der Universität Duisburg-Essen. Dort promovierte er im Themenfeld der Fußgängersimulation bei Prof. Schreckenberg. Damit war er genau der Experte, den die ptv suchte, als sie sich entschied, die Verkehrssimulations-Software im Haus um den Aspekt der Fußgängersimulation zu erweitern. Eine erste für Karlsruhe interessante Anwendung der neuen Software VISWALK war die Simulation der Großveranstaltung Das Fest hier in Karlsruhe. Die Simulation von Fußgängerströmen ist eine noch junge Disziplin. Sie entwickelte sich zunächst für Evakuierungs- und Notfall-Szenarien. Heute dient die Fußgängersimulationssoftware beispielsweise der Planung in großen Bahnhöfen. Denn hängt die Frage, ob man einen Anschlußzug kann, nicht auch von der Problematik ab, dass man dabei von anderen Fahrgästen behindert wird? Außerdem ist die Untersuchung der von Effizienz von Laufwegen sehr hilfreich in der Planung von Bauvorhaben. In der Fußgängersimulation werden verschiedene Methoden aus der Mathematik und Physik benutzt. In der Arbeitsgruppe von Herrn Schreckenberg waren es vor allem Zellularautomaten. Im nun vorhandenen Modul VISWALK wurde bei der ptv vor allem auf das Social force Modell gesetzt, das auf einem Newtonschen Ansatz (also dem Zusammenhang von Kraft und Beschleunigung) beruht und auf eine Beschreibung durch Differentialgleichungen für die einzelnen Fußgänger führt. Dieses System muss numerisch gelöst werden. Die schrittweise Lösung entspricht dabei der zeitlichen Entwicklung der Bewegung. Die Grundidee beim Social Force Modell ist, dass man sich vorstellt, dass die am Fußgänger angreifende Kräfte seine Beschleunigung (inklusive der Richtung) verändern und damit seine Bewegung bestimmen. Das einfachste Modell ist der Wunsch das Ziel zu erreichen (driving force), denn es genügt dafür eine zum gewünschten Ziel ziehende starke Kraft. Dabei muss man aber anderen Fußgängern und Hindernissen ausweichen. Das Ausweichen kann man aber leider nicht in genau ein Modell (also genau ein erwartetes Verhalten) übersetzen; es gibt dazu einfach zu viele Einflussfaktoren. Physikalisch werden sie daher als abstoßende Kräfte im Nahfeld von anderen Fußgängern und Hindernissen modelliert. Wichtige Fragen, die im Algorithmus zu berücksichtigen sind, wären beispielsweise, wie nah geht ein typischer Fußgänger typischerweise an anderen Fußgängern vorbei geht, und welche Umwege typischerweise am attraktivsten erscheinen. Aus eigener Erfahrung kennt man den inneren Kampf, wie man mit Gruppen, die sozusagen als ein weiches Hindernis im Weg stehen, umgeht. Hindurchdrängeln vermeidet man oft. Das muss auch der Algorithmus so tun, wenn er menschliches Verhalten nachbilden soll. So kann man hier die Dichte der Gruppe in eine "Härte" des Hindernisses übersetzen. Je nachdem wie dicht gepackt der Raum ist, werden solche Entscheidungen aber auch unterschiedlich ausfallen. Berechnet wird natürlich stets die Bewegung des Schwerpunkts des Fußgängers. Für die visuelle Umsetzung im Programm wird das entsprechend graphisch aufbereitet, was natürlich auch einen gewissen Rechenaufwand verursacht. Das Modell selbst ist zeitkontinuierlich und so wird die Genauigkeit durch die für das numerische Verfahren gewählte Zeitschrittweite bestimmt. Etwa 20.000 Personen können zur Zeit in Echtzeit simuliert werden. Leider ist es im Programm bisher nahezu unmöglich zu berücksichtigen, wie sich Menschen in zusammen gehörenden Zweier- oder Dreier-Gruppen bewegen. Zum Glück ist das beispielsweise in der Simulation von Berufspendlern auf einem Bahnhof ein vernachlässigbares Phänomen. Ein weiterer Aspekt ist, dass die Ergebnisse der intern komplexen Simulation sich schließlich für den Verkehrsplaner in wenig komplexen Zahlenwerten spiegeln (wie in Dichten). Dabei muss auch eine Balance gefunden werden zwischen Komplexität des Modells und der Bedienbarkeit durch einen Verkehrsplaner im Arbeitsalltag. Zu einfache Modelle - wie solche, die nur Dichten von Personen berücksichtigen (sogenannte Makromodelle) - können eventuell nicht mehr wiedergeben, dass es in Korridoren gegenläufige Bewegungen gibt, was jedoch ein zentraler Aspekt der tatsächlichen Fußgängerbewegung ist. Daten zur Kalibrierung dieser Modelle sind nicht so einfach zu erheben. Eine Möglichkeit ist die Auswertung von Videos (z.B. von Überwachungskameras). Dabei weiß man natürlich nichts über den Hintergrund der beobachteten Personen (Alter, Größe, Dringlichkeit des Ortswechsels). In Laborexperimenten sind diese Informationen verfügbar, aber es bleibt immer eine künstliche Umgebung, die die Realitäts-Nähe der Ergebnisse potentiell gefährdet. Ein noch ganz neuer dritter Weg ist in Zusammenarbeit mit der Arbeitsgruppe von Prof. Hanebeck am KIT die Beobachtung einer jeweils einzelnen echten Person in einer virtueller Umgebung am Computer. Wir unterhielten uns ausführlich über die Begleitung des Umbaus eines Straßenabschnitts in Straßburg. In dieser Stadt wurde ein grundlegender Plan piéton beschlossen, durch den sich in den Jahren 2011-2020 die Situation für alle Verkehrsteilnehmer in der Innenstadt verändern soll. Die ptv hat konkret die Umgestaltung der Brücke Pont Kuss durch Simulationen begleitet. Da die Brücke auf dem direkten Weg vom Hauptbahnhof in die historische Innenstadt liegt, ist das Fußgängeraufkommen dort besonders hoch und wurde zur Untermauerung der Notwendigkeit eines Umbaus sorgfältig gezählt. Obwohl aus den Daten klar hervorging, dass die Verteilung des öffentlichen Raums hier dringend geändert werden sollte (mehr Platz für Fußgänger, weniger Spuren für PKW) konnte darüber hinaus die Simulation zeigen, dass durch die Einengung der Fahrspuren kein zu großer Nachteil für den Autoverkehr entsteht. In der städtischen Verkehrsplanung können Schwerpunkte (wie so ein Fußgängerplan in Straßburg) häufig durch Personen in der Verwaltung stark beeinflusst werden. Die faire Verteilung von öffentlichem Raum wird uns aber in der Zukunft noch sehr stark beschäftigen. Hier ist auch die Frage der Behandlung von Radfahrern im Stadtverkehr ein Modellierungs-Problem mit vielen offenen Fragen. Die Verwendung von Simulationen in kritischen bzw. Gefahren-Situationen ist auch nicht trivial. So hat es sich als unrealistisch erwiesen, im Zeitraffer vorausberechnete Situationen als Hilfestellung für Entscheidungen zu benutzen. Man braucht in solchen Situationen Ergebnisse, die in wenigen Augenblicken gute Ratschläge geben, wie Fußgängerströme geleitet werden sollten. Das geht zum Glück häufig über Makromodelle, die nur die Dichten beachten. Dies sind einfach genug analysierbare und dabei aussagekräftige Größen in einer Krisensituation. Neue Aufgaben für die Verbesserung von Fußgänger-Simulationen stellen sich jedes Jahr. Ein wichtiger Aspekt ist im Moment, dass die Software-Umsetzung sehr viel stärker parallelisiert werden muss, um leistungsstärker werden zu können. Literatur und weiterführende Informationen
Podcasts und Videos
| |||||||||||||||||||
| 28 Apr 2016 | ÖPNV | 00:46:54 | |||||||||||||||||
Klaus Nökel arbeitet in der Firma ptvgroup an der Verkehrsmodellierung. Er war und ist an vielen Aspekten der Entwicklung der ptv-Software beteiligt. Einer seiner Schwerpunkte sind Modelle für den öffentlichen Nahverkehr - kurz ÖPNV. Oft kann man nur mit geeigneten Modellen und Simulationen den für Fördergelder erforderlichen Nachweis über einen zu erwartenden Nutzen von Baumaßnahmen erbringen. In Karlsruhe ist der Tunnel für die Straßenbahnen (in Karlsruhe kurz UStrab genannt) ein prominentes Beispiel einer solchen Großbaustelle. Die wichtigste Fragen zum erwarteten Nutzen, ist wie sich die Reisezeit verkürzt: Der Kosten-Nutzen-Quotient sollte hier natürlich möglichst klein sein. Die gesamten Baukosten sind dabei relativ einfach zu ermitteln. Die Nutzen-Seite ist dagegen nicht so einfach zu schätzen. Man braucht dafür ja Zahlen darüber, was für die Fahrgäste (quantifizierbar) besser wird- insbesondere im Bezug auf Zeiteinsparung. Um diese Frage beantworten zu können, muss für alle Einwohner eine Routenplanung für jeden Tag durchgeführt werden. In Bezug auf ÖPNV sind dies insbesondere die Mobliltätsentscheidungen zwischen Weg zu Fuß, mit dem Auto oder Fahrrad und dem ÖPNV. Das betrifft vor allem die Wege zur Arbeit, zu Freizeitaktivitäten und zum Einkaufen. Die Wohn- und Arbeitsorte liegen hier über längere Zeit fest - alle anderen Größen sind jedoch variabel und Entscheidungen wo man beispielsweise einkaufen geht, können sich mit besserer Erreichbarkeit verändern. Hier muss aufgrund vorliegender Informationen zu Wegen in der Stadt die Wahl des Verkehrsmittels modelliert werden und welche Route mit welchem Verkehrsmittel typischerweise gewählt wird. Die Frage ist dann, ob es zu Verschiebungen in der Verkehrsmittelwahl kommen wird, nachdem sich die Infrastruktur geändert hat (wie z.B. durch den Tunnel bei uns in Karlsruhe). Die Angebotsseite ist vergleichsweise einfach zu beschreiben: Verkehrsnetz(e) wie Straßen und Liniennetz des ÖPNV mit zugehörigem Fahrplan sind bekannte Daten. Die Kenntnisse über die Nachfrage sind komplex und setzen sich aus verschiedenen Anteilen zusammen. Ein gut verstandener Teil hier ist der soziodemographische z.B. ob ein Auto zur Verfügung oder nicht. Typischerweise haben junge Leute auf dem Weg zur Schule oder in die Ausbildung kein Auto zur Verfügung. Ebenso kann man gut beschreiben, wo gewohnt, gearbeitet und typischerweise eingekauft wird. Die Frage, welche Wege zurückgelegt werden, wird nicht wirklich gezählt oder genau ermittelt, sondern modelliert. Dabei sind viele Fragen nicht eindeutig beantwortbar. Manches sind auch ganz persönliche Vorlieben, so wie verschiedene Personen höhere Wegekosten gegenüber höherer Wegezeit sehr unterschiedlich gewichten. Eine typische Datenbeschaffungsmethode ist bisher, Menschen über einen gewissen Zeitraum Tagebuch zu ihren Mobilitätsentscheidungen führen zu lassen. Zusätzlich zu den so dokumentierten und hochgerechneten Entscheidungen müssen für das Modell als Vergleich auch noch mögliche Alternativen zu diesen Entscheidungen mit berechnet werden (inklusive Zeit- und Geldaufwand). Als mathematische Methode bietet sich ein Discrete Choice Modell an, denn es geht um endlich viele Alternativen zwischen denen gewählt wird. Es gibt darin einige objektive Anteile der persönlichen Nutzenfunktion und einen unbeobachtbaren Teil der Nutzenfunktion, der üblicherweise durch eine Wahrscheinlichkeitsverteilung im Modell realisiert werden kann und muss. Statistik insbesondere die Schätztheorie hilft bei der Bestimmung der Wahrscheinlichkeitsverteilungen aus vorliegenden Entscheidungen. Das Gewicht für das "Rauschen" ist eine Unbekannte im Modell. Je nach Standort für den das Modell entwickelt wird, unterscheidet sich das tatsächlich. In den letzten Jahren hat sich die Anzahl der Wahlmöglichkeiten für Mobilität durch verschiedene Sharing-Modelle außerdem stark erweitert, wie z.B. durch Carsharing oder Fahrrad-Leihe, die inzwischen auch niederschwellig und sehr flexibel geworden sind. Vor allem in Kombination mit herkömmlichen Transportmitteln liegt ein großes Potential, das gerade erschlossen wird (z.B. haben zur Zeit etwa 600 Städte in der Welt ein Leihfahrrad-System). Es wäre einfacher, wenn die Benutzung noch klarer standardisiert wäre und eine Benutzerführung so einfach wie in einer typischen App erfolgte. Sinnvoll und wünschenswert wären natürlich ausführliche Vorher-nachher-Untersuchungen, um die Güte der Vorhersagen der Modelle zu prüfen und auch zu verbessern. Bisher war das meist zu teuer, aber das ändert sich gerade, weil Datenmengen aus Smartphones nutzbar und einfach auswertbar werden. Zum Glück gibt es hier keine Berührung der Privatsphäre, weil nur anonyme Angaben aus großen Mengen von Bewegungsprofilen gebraucht werden aus denen keine Rückschlüsse auf einzelne Personen möglich sind. Die Städte versuchen für ihre Einwohner die Erreichbarkeits-Gerechtigkeit zu verbessern. Hier vereinfachen die neuen Verkehrsmittel potentiell das Problem der letzten Meile lösen zu helfen. Das Verhalten der Verkehrsteilnehmer ändert sich auch gerade in prinzipieller Weise durch die Verfügbarkeit von online-Informationen zum Verkehr (einerseits per Smartphone, andererseits durch Anzeigen an den Haltestellen). Hat man sich früher eine Variante zu Hause überlegt und so gut es ging anschließend abgearbeitet (unterwegs hatte man dabei nur beschränkt Möglichkeiten mit Verspätungen und verpassten Verbindungen fertig zu werden), so reagieren heute Fahrgäste anders, weil sie unterwegs mehr Informationen haben. Hier braucht man tatsächlich auch neue Modelle und mehr Rechenpower. Eine weitere Entwicklung ist es, im Modell zu berücksichtigen, dass Fahrgäste Entscheidungen auch nach erwartetem Komfort treffen. So sind volle Bahnen für viele abschreckend. Das könnte man im Modell noch relativ einfach berücksichtigen. Wenn man aber einbauen will, dass es eine gute Strategie ist, erst in der "falschen" Richtung zu fahren, um an einer früheren Station in die Linie einzusteigen, damit man tatsächlich auch mitkommt und nicht wegen einer überfüllten Bahn an der Haltestelle zurückbleiben muss, vergrößert das die Menge der sinnvollen Routen erheblich. Literatur und Zusatzinformationen
Podcasts und Videos
| |||||||||||||||||||
| 05 May 2016 | Viscoelastic Fluids | 00:21:11 | |||||||||||||||||
This is the second of four conversations Gudrun had during the British Applied Mathematics Colloquium which took place 5th – 8th of April 2016 in Oxford. Helen Wilson always wanted to do maths and had imagined herself becoming a mathematician from a very young age. But after graduation she did not have any road map ready in her mind. So she applied for jobs which - due to a recession - did not exist. Today she considers herself lucky for that since she took a Master's course instead (at Cambridge University), which hooked her to mathematical research in the field of viscoelastic fluids. She stayed for a PhD and after that for postdoctoral work in the States and then did lecturing at Leeds University. Today she is a Reader in the Department of Mathematics at University College London. So what are viscoelastic fluids? If we consider everyday fluids like water or honey, it is a safe assumption that their viscosity does not change much - it is a material constant. Those fluids are called Newtonian fluids. All other fluids, i.e. fluids with non-constant viscosity or even more complex behaviours, are called non-Newtonian and viscoelastic fluids are a large group among them. Already the name suggests, that viscoelastic fluids combine viscous and elastic behaviour. Elastic effects in fluids often stem from clusters of particles or long polymers in the fluid, which align with the flow. It takes them a while to come back when the flow pattern changes. We can consider that as keeping a memory of what happened before. This behaviour can be observed, e.g., when stirring tinned tomato soup and then waiting for it to go to rest again. Shortly before it finally enters the rest state one sees it springing back a bit before coming to a halt. This is a motion necessary to complete the relaxation of the soup. Another surprising behaviour is the so-called Weissenberg effect, where in a rotation of elastic fluid the stretched out polymer chains drag the fluid into the center of the rotation. This leads to a peak in the center, instead of a funnel which we expect from experiences stirring tea or coffee. The big challenge with all non-Newtonian fluids is that we do not have equations which we know are the right model. It is mostly guess work and we definitely have to be content with approximations. The simplest models then take the so-called retarded fluid assumption, i.e. the elastic properties are considered to be only weak. Then, one can expand around the Newtonian model as a base state. Of course there are a plethora of interesting questions connected to complex fluids. The main question in the work of Helen Wilson is the stability of the flow of those fluids in channels, i.e. how does it react to small perturbations? Do they vanish in time or could they build up to completely new flow patterns? In 1999, she published results of her PhD thesis and predicted a new type of instability for a shear-thinning material model. It was to her great joy when in 2013 experimentalists found flow behaviour which could be explained by her predicted instability. More precisely, in the 2013 experiments a dilute polymer solution was sent through a microchannel. The material model for the fluid is shear thinning as in Helen Wilson's thesis. They observed oscillations from side to side of the channel and surprising noise in the maximum flow rate. This could only be explained by an instability which they did not know about at that moment. In a microchannel inertia is negligible and the very low Reynolds number of Of course, even for the easiest non-linear models one arrives at highly non-linear equations. In order to analyse stability of solutions to them one firstly needs to know the corresponding steady flow. Fortunately, if starting with the easiest non-linear models in a channel one can still find the steady flow as an analytic solution with paper and pencil since one arrives at a 1D ODE, which is independent of time and one of the two space variables. The next question then is: How does it respond to small perturbation? The classical procedure is to linearize around the steady flow which leads to a linear problem to solve in order to know the stability properties. The basic (steady) flow allows for Fourier transformation which leads to a problem with two scalar parameters - one real and one complex. The general structure is an eigenvalue problem which can only be solved numerically. After we know the eigenvalues we know about the (so-called linear) stability of the solution. An even more interesting research area is so-called non-linear stability. But it is still an open field of research since it has to keep the non-linear terms. The difference between the two strategies (i.e. linear and non-linear stability) is that the linear theory predicts instability to the smallest perturbations but the non-linear theory describes what happens after finite-amplitude instability has begun, and can find larger instability regions. Sometimes (but unfortunately quite rarely) both theories find the same point and we get a complete picture of when a stable region changes into an unstable one. One other really interesting field of research for Helen Wilson is to find better constitutive relations. Especially since the often used power law has inbuilt unphysical behaviour (which means it is probably too simple). For example, taking a power law with negative exponent says that In the middle of the flow there is a singularity (we would divide by zero) and perturbations are not able to cross the center line of a channel. Also, it is unphysical that according to the usual models the shear-thinning fluid should be instantly back to a state of high viscosity after switching off the force. For example most ketchup gets liquid enough to serve it only when we shake it. But it is not instantly thick after the shaking stops - it takes a moment to solidify. This behaviour is called thixotropy. Literature and additional material
| |||||||||||||||||||
| 26 May 2016 | Verkehrsmodellierung I | 00:17:27 | |||||||||||||||||
Peter Vortisch bekleidet seit 2010 eine Professur für Verkehrswesen am Karlsruher Institut für Technologie (KIT) und ist Leiter des Instituts für Verkehrswesen. Wir haben über die Entwicklung der Modellierung von Verkehr gesprochen und dabei den Schwerpunkt zunächst auf die Anfangszeit gelegt, in der sich die in der Forschung geborene Idee Schritt für Schritt in ein Softwareprodukt entwickelte und wo und warum sich die Idee und das Produkt durchsetzen konnten. Peter Vortisch hat in Karlsruhe eigentlich Informatik studiert und kam zum Verkehrswesen zunächst als wissenschaftliche Hilfskraft. Er hat dann bald mit an den ersten Simulationen programmiert. Solche Simulationen wurden damals auf Großrechnern durchgeführt, von denen es nur wenige gab. Die Forschungen und theoretischen wie praktischen Überlegungen wurden im wesentlichen von Professor Wiedemann vorangetrieben. Seine Karlsruher Gruppe war die erste, die das in Deutschland erfolgreich erprobte und schließlich als Standard eingeführt hat. Es gab damals Forschungsprojekte z.B. zur Wirkung von Tempolimits im Auftrag des Verkehrsministeriums. In der Zwischenzeit entwickelte sich die Rechentechnik weiter und mit dem Siegeszug des PCs wanderte die Simulation vom Rechenzentrum auf die Schreibtische. Damals war es möglich, auf so einem Rechner ein Modell mit etwa 20 Fahrzeugen in Echtzeit zu simulieren - heut sind die Rechner so viel schneller, dass mehrere 100.000 Fahrzeuge möglich sind. Aber auch mit so wenigen Fahrzeugen war es ein wichtiger Schritt hin zur Kommerzialisierung der Verkehrsmodelle. In den USA gab es damals z.B. ein öffentlich subventioniertes Produkt für Verkehrsplaner, was einen durchschlagenden Erfolg hatte und die Simulation in allen Büros etablierte. In Karlsruhe entwickelte sich ein Spin off aus dem Institut, die Firma ptv entwickelte das Produkt und die Vermarktung der Verkehrssimultion zunächst in Deutschland. Seither besteht eine enge Zusammenarbeit mit dem Institut für Verkehrswesen. Im Zuge dieser Professionalisierung wurde die Verwendung des Produktes durch Verkehrsingenieure der neue Standard. Es gab zwei große deutsche Unternehmen, die die Entwicklung der Software stark beschleunigt haben. Zunächst die Firma SIEMENS weil sie die Wirkung von Ampelsteuerungen besser vorhersehen wollte. U.a. auch im Zusammenhang mit der Grün-Anforderung durch den ÖPNV. Vor dem Aufbau auf einer echter Kreuzung sollte die Simulation auf dem Rechner beweisen, dass auch der gewünschte Effekt durch die Ampelsteuerung erreicht werden würde. Das wurde schließlich sogar Teil der SIEMENS Software Verkehrsplanung. Verkehrsplaner in den Städten haben in dieser Zeit weitergehende Ideen noch nicht so gut angenommen. Dafür war dann die Firma Volkswagen ein Vorreiter. Sie hat sich eigentlich für Abgasemissionen interessiert, wofür man Temperaturverläufe der Motoren braucht. Es wurde daraus die Aufgabe abgeleitet, für eine ganze Stadt den Verkehr über den Tag hinweg zu simulieren (inkl. parken). Sie haben sich in großem Umfang finanziell an den Entwicklungsarbeiten beteiligt. Prototyp wurde die Stadt Braunschweig. Ohne die heute selbstverständlich vorliegenden Daten zu Straßen und Kreuzungen war das ein sehr aufwändiges Vorhaben. Außerdem brauchte man neue Verfahren, die entscheiden, welche Wege die Fahrzeuge in der Stadt zurücklegend. Ein wichtiges neues Verfahren hierfür wurde die Dynamische Umlegung. Diese neue Fähigkeit des Programms hat zu einer deutlich weiteren Verbreitung geführt, denn es war nun ein wirklich professionelles Softwareprodukt auf dem Markt in Deutschland vorhanden. Der Funktionsumfang des ptv-Produktes war schließlich größer als das des USA-Standards. Da dort Verkehrssimulation aber schon Usus war, war es einfach mit dem noch besseren Produkt in den US-Markt einzusteigen. Ein weiterer wichtiger Markt war auch Großbritannien, da dort traditionell bei Planungen viel modelliert wird ("Mutterland der Modellierung"). Dort war der Einstieg geschafft, als sich Transport for London entschied, mit dem ptv-Produkt zu arbeiten. Podcasts und Videos
| |||||||||||||||||||
| 02 Jun 2016 | Banach-Tarski Paradox | 00:27:47 | |||||||||||||||||
Nicolas Monod teaches at the École polytechnique fédérale in Lausanne and leads the Ergodic and Geometric Group Theory group there. In May 2016 he was invited to give the Gauß lecture of the German Mathematical Society (DMV) at the Technical University in Dresden. He presented 100 Jahre Zweisamkeit – The Banach-Tarski Paradox. The morning after his lecture we met to talk about paradoxes and hidden assumptions our mind makes in struggling with geometrical representations and measures. A very well-known game is Tangram. Here a square is divided into seven pieces (which all are polygons). These pieces can be rearranged by moving them around on the table, e.g.. The task for the player is to form given shapes using the seven pieces – like a cat etc.. Of course the Tangram cat looks more like a flat Origami-cat. But we could take the Tangram idea and use thousands or millions of little pieces to build a much more realistic cat with them – as with pixels on a screen. In three dimensions one can play a similar game with pieces of a cube. This could lead to a LEGO-like three-dimensional cat for example. In this traditional Tangram game, there is no fundamental difference between the versions in dimension two and three. But in 1914 it was shown that given a three-dimensional ball, there exists a decomposition of this ball into a finite number of subsets, which can then be rearranged to yield two identical copies of the original ball. This sounds like a magical trick – or more scientifically said – like a paradoxical situation. It is now known under the name Banach-Tarski paradox. In his lecture, Nicolas Monod dealt with the question: Why are we so surprised about this result and think of it as paradoxical? One reason is the fact that we think to know deeply what we understand as volume and expect it to be preserved under rearrangements (like in the Tangram game, e.g.).Then the impact of the Banach-Tarski paradox is similar for our understanding of volume to the shift in understanding the relation between time and space through Einstein's relativity theory (which is from about the same time). In short the answer is: In our every day concept of volume we trust in too many good properties of it. It was Felix Hausdorff who looked at the axioms which should be valid for any measure (such as volume). It should be independent of the point in space where we measure (or the coordinate system) and if we divide objects, it should add up properly. In our understanding there is a third hidden property: The concept "volume" must make sense for every subset of space we choose to measure. Unfortunately, it is a big problem to assign a volume to any given object and Hausdorff showed that all three properties cannot all be true at the same time in three space dimensions. Couriously, they can be satisfied in two dimensions but not in three. Of course, we would like to understand why there is such a big difference between two and three space dimensions, that the naive concept of volume breaks down by going over to the third dimension. To see that let us consider motions. Any motion can be decomposed into translations (i.e. gliding) and rotations around an arbitrarily chosen common center. In two dimensions the order in which one performs several rotations around the same center does not matter since one can freely interchange all rotations and obtains the same result. In three dimensions this is not possible – in general the outcomes after interchanging the order of several rotations will be different. This break of the symmetry ruins the good properties of the naive concept of volume. Serious consequences of the Banach-Tarski paradox are not that obvious. Noone really duplicated a ball in real life. But measure theory is the basis of the whole probability theory and its countless applications. There, we have to understand several counter-intuitive concepts to have the right understanding of probabilities and risk. More anecdotally, an idea of Bruno Augenstein is that in particle physics certain transformations are reminiscent of the Banach-Tarski phenomenon. Nicolas Monod really enjoys the beauty and the liberty of mathematics. One does not have to believe anything without a proof. In his opinion, mathematics is the language of natural sciences and he considers himself as a linguist of this language. This means in particular to have a closer look at our thought processes in order to investigate both the richness and the limitations of our models of the universe. References:
| |||||||||||||||||||